Chào mừng bạn đến với bài học về Lý thuyết Giới hạn của dãy số, một trong những chủ đề quan trọng của chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và nâng cao về giới hạn dãy số, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và được trình bày một cách trực quan, giúp bạn tiếp thu kiến thức một cách nhanh chóng và hiệu quả.
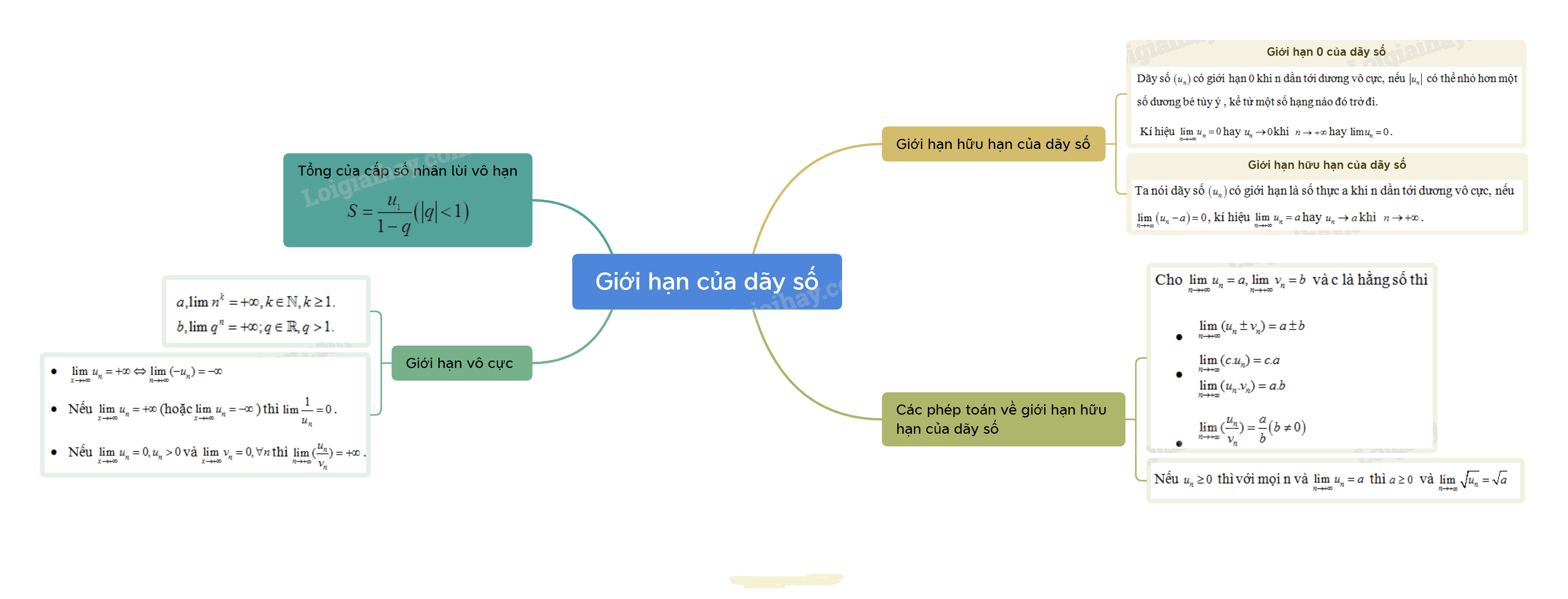
1, Giới hạn hữu hạn của dãy số
1, Giới hạn hữu hạn của dãy số
a, Giới hạn 0 của dãy số
- Dãy số \(\left( {{u_n}} \right)\) có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.
Kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0\) hay \({u_n} \to 0\)khi \(n \to + \infty \) hay \(\lim {u_n} = 0\).
* Chú ý:
+ \(\lim \frac{1}{{{n^k}}} = 0,k \in \mathbb{Z}.\)
+ Nếu \(\left| q \right| < 1\) thì \(\lim {q^n} = 0\)
b, Giới hạn hữu hạn của dãy số
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) hay \({u_n} \to a\) khi \(n \to + \infty \).
* Chú ý: Nếu \({u_n} = c\)(c là hằng số) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = c\)
2. Các phép toán về giới hạn hữu hạn của dãy số
Cho \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) và c là hằng số thì
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn là:
\(S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)\)
4. Giới hạn vô cực
- Dãy số \(\left( {{u_n}} \right)\)được gọi là có giới hạn \( + \infty \)khi \(n \to + \infty \)nếu \({u_n}\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \) hay \({u_n} \to + \infty \) khi \(n \to + \infty \).
- Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( - \infty \)khi \(n \to + \infty \) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left( { - {u_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = - \infty \) hay \({u_n} \to - \infty \) khi \(n \to + \infty \).
* Chú ý:
*Nhận xét:
\(\begin{array}{l}a,\lim {n^k} = + \infty ,k \in \mathbb{N},k \ge 1.\\b,\lim {q^n} = + \infty ;q \in \mathbb{R},q > 1.\end{array}\)
Giới hạn của dãy số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc xây dựng các khái niệm toán học phức tạp hơn như đạo hàm, tích phân. Trong chương trình Toán 11 Chân trời sáng tạo, việc nắm vững lý thuyết này là điều kiện cần thiết để giải quyết các bài toán liên quan đến dãy số và chuỗi số.
Một dãy số (un) được gọi là có giới hạn hữu hạn L nếu với mọi ε > 0, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có |un - L| < ε. Ký hiệu: limn→∞ un = L.
Dãy số (un) được gọi là có giới hạn vô cực dương (âm) nếu với mọi M > 0, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có un > M (un < -M). Ký hiệu: limn→∞ un = +∞ (limn→∞ un = -∞).
Ví dụ 1: Tính limn→∞ (2n + 1) / (n - 3).
Giải: limn→∞ (2n + 1) / (n - 3) = limn→∞ (2 + 1/n) / (1 - 3/n) = 2/1 = 2.
Ví dụ 2: Tính limn→∞ (1/2)n.
Giải: Vì |1/2| < 1 nên limn→∞ (1/2)n = 0.
Hãy tự giải các bài tập sau để củng cố kiến thức về giới hạn của dãy số:
Lý thuyết Giới hạn của dãy số là một công cụ quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về sự hội tụ và phân kỳ của các dãy số. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán phức tạp hơn trong chương trình Toán 11 Chân trời sáng tạo và các chương trình toán học nâng cao.