Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1, chương trình Chân trời sáng tạo.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 102, 103, 104, 105. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
a) Trong không gian, cho điểm \(M\) ở ngoài đường thẳng \(d\). Đặt \(\left( P \right) = mp\left( {M,d} \right)\). Trong \(\left( P \right)\), qua \(M\) vẽ đường thẳng \(d'\) song song với \(d\), đặt \(\left( Q \right) = mp\left( {d,d'} \right)\). Có thể khẳng định hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau không?
a) Trong không gian, cho điểm \(M\) ở ngoài đường thẳng \(d\). Đặt \(\left( P \right) = mp\left( {M,d} \right)\). Trong \(\left( P \right)\), qua \(M\) vẽ đường thẳng \(d'\) song song với \(d\), đặt \(\left( Q \right) = mp\left( {d,d'} \right)\). Có thể khẳng định hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau không?
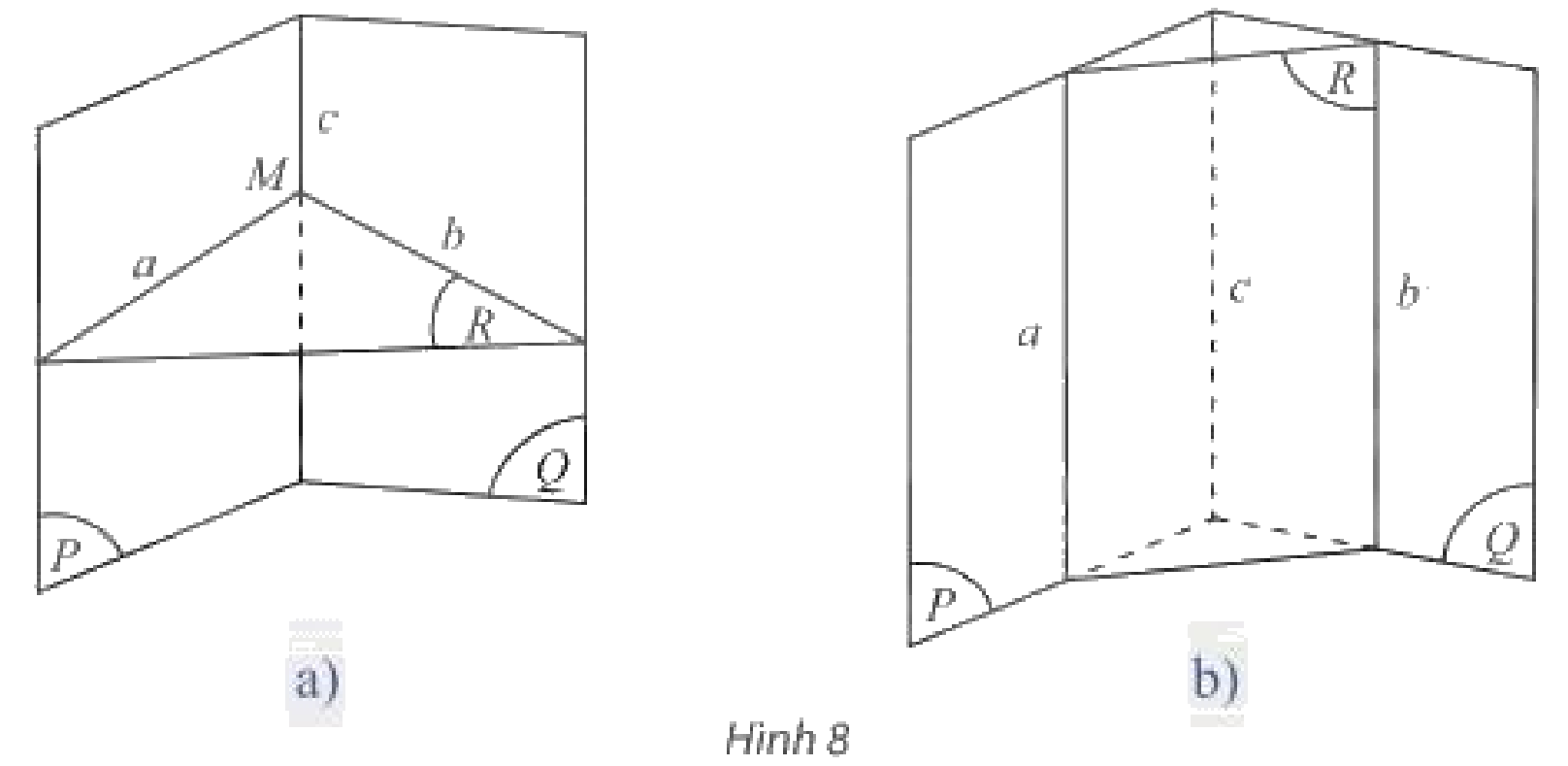
b) Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) cắt nhau theo ba giao tuyến \(a,b,c\) phân biệt với \(a = \left( P \right) \cap \left( R \right);b = \left( Q \right) \cap \left( R \right);c = \left( P \right) \cap \left( Q \right)\) (Hình 8).
Nếu \(a\) và \(b\) có điểm chung \(M\) thì điểm \(M\) có thuộc \(c\) không?
Phương pháp giải:
Áp dụng tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Lời giải chi tiết:
a) Theo đề bài ta có: \(d' \subset \left( P \right),d' \subset \left( Q \right)\) nên \(d'\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Lại có: \(d \subset \left( P \right),d \subset \left( Q \right)\) nên \(d\) cũng là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Theo tính chất thừa nhận 5: hai mặt phẳng phân biệt có một đường thẳng chung duy nhất. Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in a\\a \subset \left( P \right)\end{array} \right\} \Rightarrow M \in \left( P \right)\\\left. \begin{array}{l}M \in b\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\end{array}\)
Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in c\).
Cho hình chóp \(S.ABCD\). Vẽ hình thang \(A{\rm{D}}M{\rm{S}}\) có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\). Gọi \(d\) là đường thẳng trong không gian đi qua \({\rm{S}}\) và song song với \(A{\rm{D}}\). Chứng minh đường thẳng \(d\) nằm trong mặt phẳng \(\left( {SAD} \right)\).
Phương pháp giải:
Sử dụng:
‒ Định lí 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
‒ Tính chất: Có duy nhất một mặt phẳng chứa hai đường thẳng song song.
Lời giải chi tiết:

\(A{\rm{D}}M{\rm{S}}\) là hình thang có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\) nên \(A{\rm{D}}\parallel M{\rm{S}}\).
Theo đề bài ta lại có \(d\parallel A{\rm{D}}\).
Do đó \(d \equiv MS\) (theo định lí 1).
Lại có: \(SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)\).
Ta đã biết trong cùng một mặt phẳng, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau (Hình 13a).
Trong không gian, cho ba đường thẳng không đồng phẳng, \(a\) và \(b\) cùng song song với \(c\). Gọi \(M\) là điểm thuộc \(a\), \(d\) là giao tuyến của \(mp\left( {a,c} \right)\) và \(mp\left( {M,b} \right)\) (Hình 13b). Do \(b\parallel c\) nên ta có \(d\parallel b\) và \(d\parallel c\). Giải thích tại sao \(d\) phải trùng với \(a\). Từ đó, nêu kết luận về vị trí giữa \(a\) và \(b\).

Phương pháp giải:
Sử dụng định lí 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết:
Ta có: \(d = mp\left( {a,c} \right) \cap mp\left( {M,b} \right) \Rightarrow M \in d\)
Lại có: \(M \in a\)
Mà qua \(M\) chỉ có một đường thẳng song song với đường thẳng \(b\) nên \(d \equiv a\).
Do đó \(a\parallel b\).
Cho tứ diện \(ABCD\) có \(I\) và \(J\) lần lượt là trung điểm của các cạnh \(BC\) và \(B{\rm{D}}\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(I,J\) và cắt hai cạnh \(AC\) và \(A{\rm{D}}\) lần lượt tại \(M\) và \(N\).
a) Chứng minh \(IJNM\) là một hình thang.
b) Tìm vị trí của điểm \(M\) dễ \(IJNM\) là hình bình hành.

Phương pháp giải:
Sử dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đổi một song song.
Lời giải chi tiết:
a) Ta có: \(I\) là trung điểm của \(BC\)
\(J\) là trung điểm của \(B{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(BCD\)
\( \Rightarrow IJ\parallel CD,IJ = \frac{1}{2}C{\rm{D}}\)
Ta có:
\(\begin{array}{l}IJ = \left( {BC{\rm{D}}} \right) \cap \left( P \right)\\MN = \left( {AC{\rm{D}}} \right) \cap \left( P \right)\\C{\rm{D}} = \left( {AC{\rm{D}}} \right) \cap \left( {BC{\rm{D}}} \right)\\IJ\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(IJ\parallel MN\parallel C{\rm{D}}\).
Vậy \(IJNM\) là hình thang.
b) Để \(IJNM\) là hình bình hành thì \(IJ = MN\).
Mà \(IJ = \frac{1}{2}CD\) nên \(MN = \frac{1}{2}CD\).
Khi đó \(MN\) là đường trung bình của tam giác \(ACD\).
\( \Rightarrow M\) trung điểm của AC.
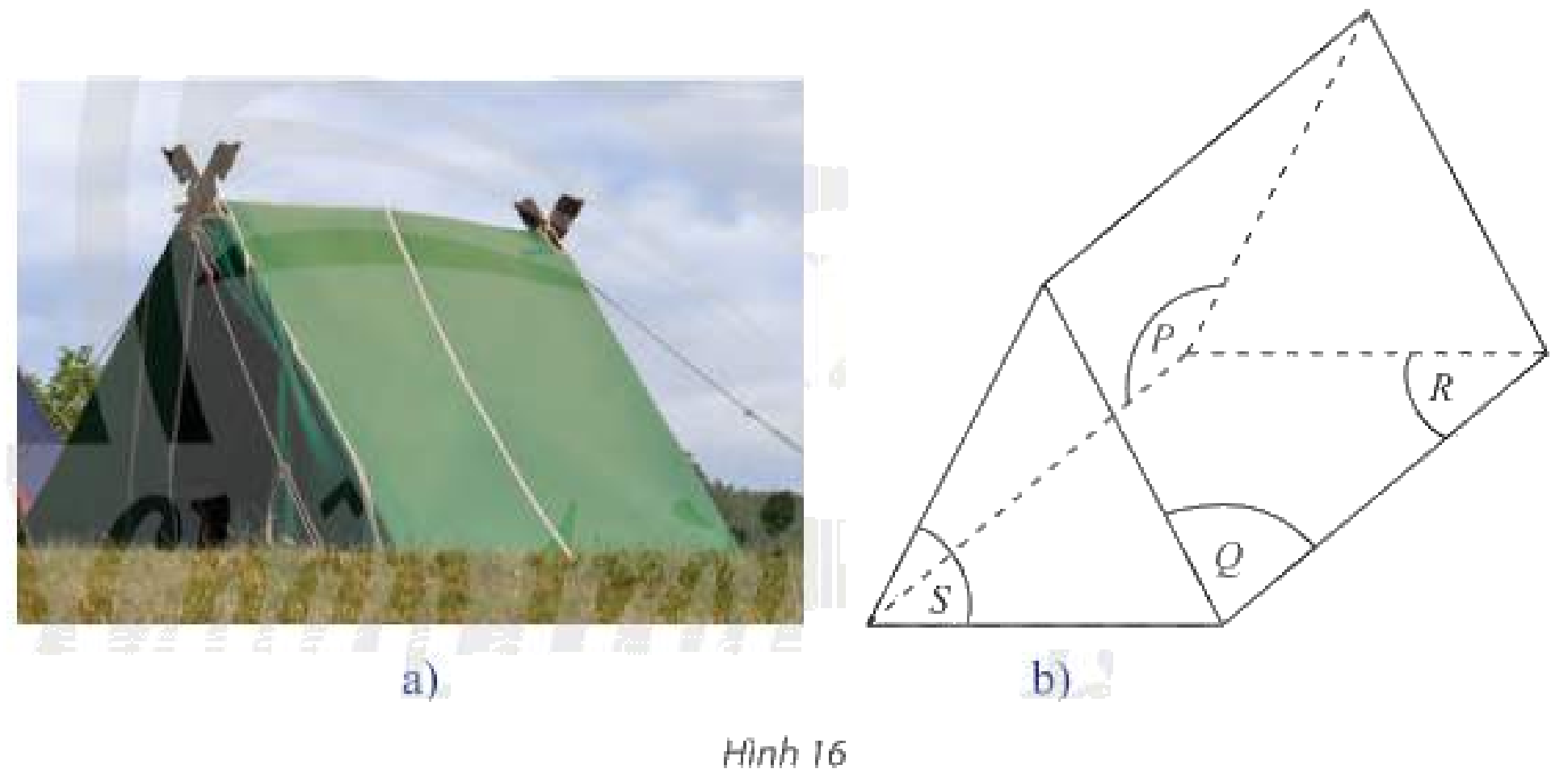
Một chiếc lều (Hình 16a) được minh hoạ như Hình 16b.
a) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song.
b) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy.

Phương pháp giải:
Áp dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
Lời giải chi tiết:
a) Ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song là: \(\left( P \right),\left( Q \right),\left( R \right)\).
b) Ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy là: \(\left( P \right),\left( Q \right),\left( S \right)\).
Mục 2 của SGK Toán 11 tập 1 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các giải thích rõ ràng, giúp học sinh hiểu sâu sắc kiến thức và áp dụng vào các bài toán tương tự.
Các bài tập trên trang 102 thường là các bài tập áp dụng trực tiếp các định nghĩa, định lý đã học. Ví dụ, có thể là bài tập về xác định các yếu tố của một hàm số, vẽ đồ thị hàm số, hoặc tìm tập xác định, tập giá trị của hàm số. Lời giải sẽ đi kèm với các bước thực hiện cụ thể, giúp học sinh dễ dàng theo dõi và hiểu được cách giải.
Trang 103 có thể chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết. Ví dụ, có thể là bài tập về tìm điều kiện để một phương trình có nghiệm, hoặc chứng minh một bất đẳng thức. Lời giải sẽ tập trung vào việc phân tích bài toán, tìm ra hướng giải phù hợp và trình bày một cách logic, rõ ràng.
Các bài tập trên trang 104 thường liên quan đến việc giải các bài toán thực tế, ứng dụng kiến thức toán học vào các tình huống cụ thể. Ví dụ, có thể là bài toán về tính toán diện tích, thể tích, hoặc giải các bài toán về chuyển động. Lời giải sẽ tập trung vào việc mô hình hóa bài toán, xây dựng phương trình toán học và giải phương trình đó để tìm ra kết quả.
Trang 105 thường là phần bài tập tổng hợp, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Các bài tập trên trang này có thể bao gồm nhiều dạng khác nhau, đòi hỏi học sinh phải có khả năng phân tích, tổng hợp và vận dụng kiến thức một cách linh hoạt. Lời giải sẽ cung cấp các phương pháp giải khác nhau, giúp học sinh lựa chọn phương pháp phù hợp nhất để giải quyết bài toán.
Ngoài SGK Toán 11 tập 1 chương trình Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những lời giải chi tiết, dễ hiểu và hữu ích cho các bài tập trong mục 2 trang 102, 103, 104, 105 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!