Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 67, 68, 69 sách giáo khoa Toán 11 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho đường thẳng (a) vuông góc với mặt phẳng (left( Q right)).
Cho đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\). Mặt phẳng \(\left( P \right)\) chứa \(a\) và cắt \(\left( Q \right)\) theo giao tuyến \(c\). Trong \(\left( Q \right)\) ta vẽ đường thẳng \(b\) vuông góc với \(c\).
Hỏi:
a) \(\left( P \right)\) có vuông góc với \(\left( Q \right)\) không?
b) Đường thẳng \(b\) vuông góc với \(\left( P \right)\) không?
Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)\)
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:

a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?
b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?
Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)
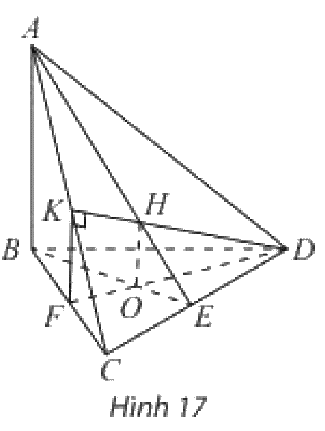
Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:

a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);
b) \(OH \bot \left( {ADC} \right)\).
Phương pháp giải:
‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng:
+ Cách 1: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
+ Cách 2: sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)
Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.
Phương pháp giải:
Sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết:
Ta mở quyển sách ra và đặt quyển sách lên mặt bàn sao cho hai mép dưới của bìa sách nằm trên mặt bàn.
Mục 3 trong SGK Toán 11 tập 2 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Cụ thể, các em sẽ được làm quen với các khái niệm như đạo hàm tại một điểm, đạo hàm của hàm số, quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán liên quan đến đạo hàm trong chương trình Toán 11 và các chương trình nâng cao.
Các bài tập trên trang 67 chủ yếu yêu cầu học sinh tính đạo hàm của hàm số tại một điểm cụ thể. Để giải quyết các bài tập này, các em cần áp dụng định nghĩa đạo hàm: f'(x₀) = lim (h→0) [f(x₀ + h) - f(x₀)] / h. Việc tính toán giới hạn này đòi hỏi sự cẩn thận và chính xác.
Trang 68 tập trung vào việc tìm đạo hàm của các hàm số đơn giản. Các em cần sử dụng các quy tắc tính đạo hàm cơ bản như đạo hàm của hàm số lũy thừa, đạo hàm của hàm số lượng giác, và đạo hàm của hàm số mũ.
Trang 69 đưa ra các bài tập áp dụng quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp. Đây là những bài tập đòi hỏi sự hiểu biết sâu sắc về các quy tắc đạo hàm và khả năng vận dụng linh hoạt.
Ví dụ: Tìm đạo hàm của hàm số f(x) = (x² + 1) * sin(x). Để giải bài tập này, các em cần sử dụng quy tắc đạo hàm của tích: (u * v)' = u' * v + u * v'.
Để giải các bài tập về đạo hàm một cách hiệu quả, các em nên:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập về đạo hàm trong SGK Toán 11 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!