Chào mừng bạn đến với bài học về Lý thuyết Phép chiếu song song, một phần quan trọng trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về phép chiếu song song, giúp bạn hiểu rõ hơn về hình học không gian.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến những bài giảng chất lượng, dễ hiểu, cùng với các bài tập thực hành đa dạng để bạn có thể tự tin chinh phục môn Toán.
Lý thuyết Phép chiếu song song
1. Khái niệm phép chiếu song song
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) sao cho MM’ song song hoặc trùng với \(l\) được gọi là phép chiếu song songlên mặt phẳng \(\left( P \right)\) theo phương \(l\).
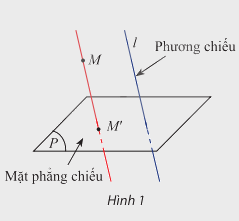
- Mặt phẳng \(\left( P \right)\) gọi là mặt phẳng chiếu, đường thẳng \(l\) gọi là phương chiếu, điểm M’ gọi là hình chiếu song song (hoặc ảnh) của điểm M qua phép chiếu theo phương \(l\).
- Cho hình \(\Re \), tập hợp \(\Re '\) các ảnh M’ của tất cả những điểm M thuộc \(\Re \)qua phép chiếu song song được gọi là hình chiếu song song của \(\Re \) lên mặt phẳng (P).
2. Các tính chất cơ bản của phép chiếu song song
- Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng, biến tia thành tia.
- Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.
- Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó.
- Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng cùng nằm trên hai đường thẳng song song hoặc trùng nhau.
3. Hình biểu diễn của một hình không gian
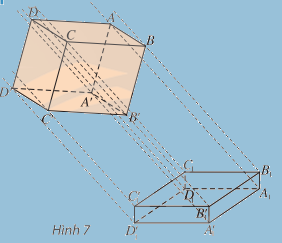
- Nếu trên hình có 2 đoạn thẳng nằm trên 2 đường thẳng song song (trùng nhau) thì chúng được biểu diễn bằng 2 đoạn thẳng nằm trên 2 đường thẳng song song (trùng nhau) và tỉ số độ dài của 2 đoạn thẳng không đổi.
- Nếu hình phẳng nằm trong mặt phẳng không song song với phương chiếu thì:
+ Hình biểu diễn của một đường tròn là một elip.
+ Hình biểu diễn của một tam giác (vuông, cân, đều) là một tam giác.
+ Hình biểu diễn của hình vuông, hình chữ nhật, hình thoi, hình bình hành là hình bình hành.
Phép chiếu song song là một phép biến hình quan trọng trong hình học không gian, đóng vai trò nền tảng để hiểu và giải quyết nhiều bài toán liên quan đến vị trí tương đối của các điểm, đường thẳng và mặt phẳng. Bài viết này sẽ trình bày chi tiết lý thuyết về phép chiếu song song theo chương trình Toán 11 Chân trời sáng tạo, bao gồm định nghĩa, tính chất, và ứng dụng.
Phép chiếu song song lên một mặt phẳng (P) theo phương l là một phép biến hình biến mỗi điểm M trong không gian thành điểm M’ trên (P) sao cho đường thẳng MM’ song song với l.
Phép chiếu song song bảo toàn:
Một trường hợp đặc biệt của phép chiếu song song là phép chiếu vuông góc, trong đó phương chiếu l vuông góc với mặt phẳng chiếu (P). Phép chiếu vuông góc có những tính chất đặc biệt hơn, như bảo toàn độ dài đoạn thẳng.
Phép chiếu song song có nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học, bao gồm:
Bài 1: Cho hình chóp S.ABCD. Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABCD). Hãy xác định hình chiếu song song của điểm S lên mặt phẳng (ABCD) theo phương SH.
Bài 2: Cho hai đường thẳng song song a và b. Hãy chứng minh rằng hình chiếu song song của a và b lên một mặt phẳng (P) theo một phương bất kỳ cũng là hai đường thẳng song song.
Lý thuyết phép chiếu song song là bước đệm quan trọng để học các phép biến hình khác trong không gian, như phép đối xứng, phép quay, và phép tịnh tiến. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và chính xác hơn.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Phép chiếu song song - SGK Toán 11 Chân trời sáng tạo. Hãy luyện tập thêm các bài tập để củng cố kiến thức và tự tin hơn trong quá trình học tập.