Chào mừng bạn đến với bài học về lý thuyết Đường thẳng vuông góc với mặt phẳng trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về mối quan hệ giữa đường thẳng và mặt phẳng trong không gian.
Chúng ta sẽ cùng nhau tìm hiểu các định nghĩa, tính chất, dấu hiệu nhận biết và ứng dụng của đường thẳng vuông góc với mặt phẳng. Bài học được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức.
1. Đường thẳng vuông góc với mặt phẳng
1. Đường thẳng vuông góc với mặt phẳng
Định nghĩa: Đường thẳng d được gọi là vuông góc với mặt phẳng \(\left( \alpha \right)\) nếu d vuông góc với mọi đường thẳng nằm trong \(\left( \alpha \right)\), kí hiệu \(d \bot \left( \alpha \right)\).
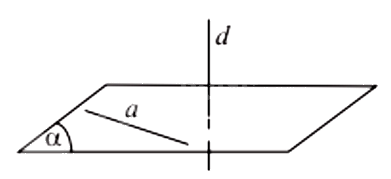
Định lí 1:
Nếu một đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
Định lí 2:
- Có duy nhất một mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước.
- Có duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.
2. Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng
Định lí 3:
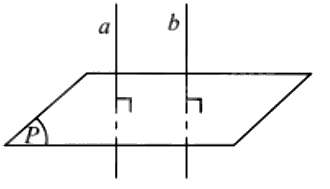
a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Định lí 4:
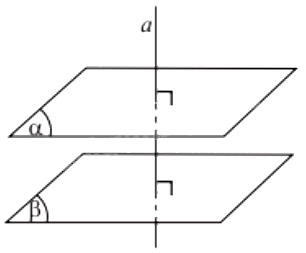
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Định lí 5:
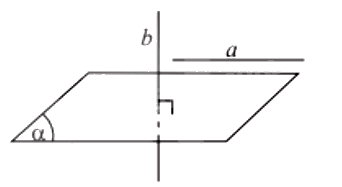
a) Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\). Đường thẳng nào vuông góc với \(\left( \alpha \right)\) thì cũng vuông góc với a.
b) Nếu đường thẳng a và mặt phẳng \(\left( \alpha \right)\) (không chứa a) cũng vuông góc với một đường thẳng b thì chúng song song với nhau.
3. Phép chiếu vuông góc
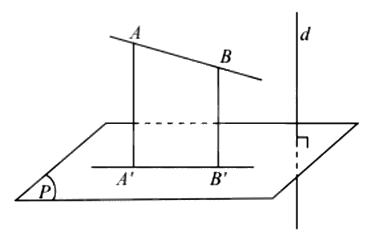
Định nghĩa: Cho mặt phẳng (P) và đường thẳng d vuông góc với (P). Phép chiếu song song theo phương của d lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên (P).
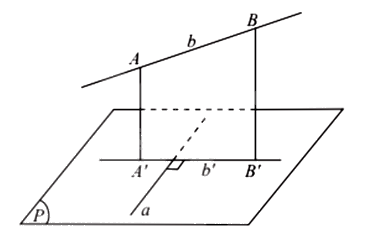
Định lí ba đường vuông góc
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b’ là hình chiếu vuông góc của b trên (P). Khi đó a vuông góc với b khi và chỉ khi a vuông góc với b’.
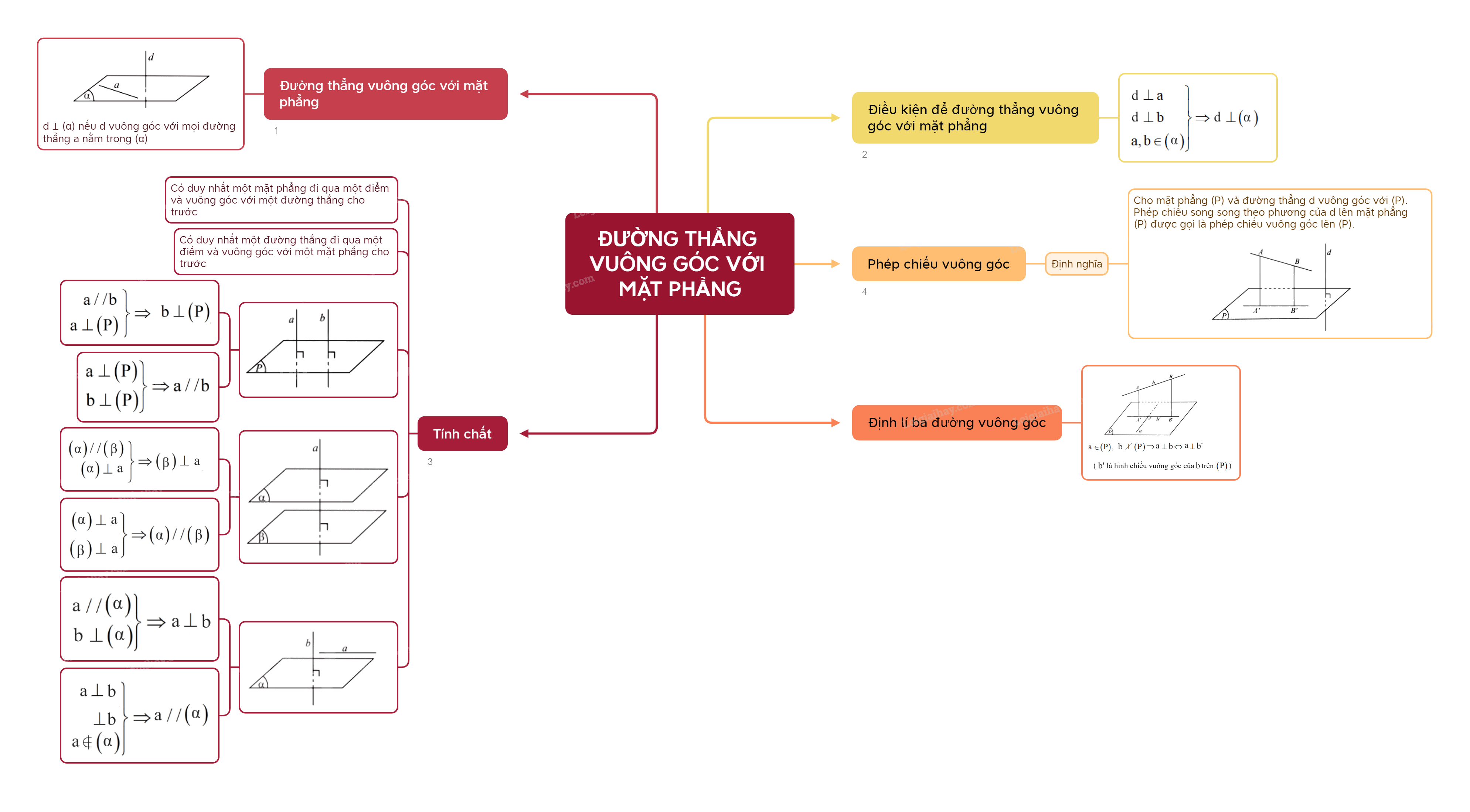
Trong chương trình Hình học không gian lớp 11, chủ đề về đường thẳng vuông góc với mặt phẳng đóng vai trò then chốt. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến chủ đề này là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các kiến thức nâng cao hơn.
Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Điều kiện để đường thẳng d vuông góc với mặt phẳng (P) là d vuông góc với hai đường thẳng cắt nhau nằm trong (P).
Có nhiều dấu hiệu để nhận biết một đường thẳng vuông góc với một mặt phẳng. Một số dấu hiệu quan trọng bao gồm:
Khi một đường thẳng d không vuông góc với mặt phẳng (P), ta có khái niệm về đường thẳng xiên và hình chiếu của đường thẳng d lên mặt phẳng (P). Độ dài của đường thẳng xiên luôn lớn hơn độ dài của hình chiếu của nó lên mặt phẳng (P).
Các bài toán liên quan đến đường thẳng vuông góc với mặt phẳng thường yêu cầu:
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Giải: Vì SA vuông góc với (ABCD) nên SA vuông góc với AC. Do đó, tam giác SAC vuông tại A. Góc giữa SC và (ABCD) là góc SCA. Ta có tan SCA = SA/AC = SA/(a√2). Từ đó suy ra góc SCA.
Để củng cố kiến thức, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững lý thuyết và kỹ năng giải bài tập một cách hiệu quả.
Lý thuyết về đường thẳng vuông góc với mặt phẳng là một phần quan trọng của chương trình Hình học không gian lớp 11. Việc hiểu rõ các định nghĩa, tính chất, dấu hiệu nhận biết và ứng dụng của đường thẳng vuông góc với mặt phẳng sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và chính xác. Chúc bạn học tốt!