Bài 4 trang 81 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4 trang 81 SGK Toán 11 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Cho hình lăng trụ tam giác đều (ABC.A'B'C') có (AB = a), góc giữa hai mặt phẳng (left( {A'BC} right)) và (left( {ABC} right)) bằng ({60^ circ }).
Đề bài
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \({60^ \circ }\).
a) Tính khoảng cách giữa hai đáy của hình lăng trụ.
b) Tinh thể tích của khối lăng trụ.
Phương pháp giải - Xem chi tiết
‒ Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách một điểm nằm trên mặt phẳng này đến mặt phẳng còn lại.
‒ Công thức tính thể tích khối lăng trụ: \(V = Sh\).
Lời giải chi tiết
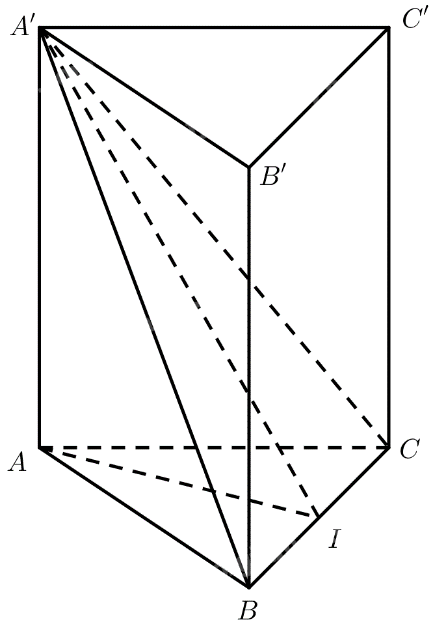
a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)
Bài 4 trang 81 SGK Toán 11 tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 4 yêu cầu học sinh giải các bài toán về đạo hàm, cụ thể là tính đạo hàm của hàm số, tìm điểm cực trị, và khảo sát hàm số. Các bài toán thường được trình bày dưới dạng các hàm số đơn giản, nhưng đòi hỏi học sinh phải áp dụng đúng các công thức và kỹ năng đã học.
Để giải Bài 4 trang 81 SGK Toán 11 tập 2, học sinh cần thực hiện các bước sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
Khi giải Bài 4 trang 81 SGK Toán 11 tập 2, học sinh cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về đạo hàm, học sinh có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 81 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đạo hàm và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.