Bài 7 trang 98 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Cấp số cho và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán liên quan đến cấp số, tìm số hạng tổng quát và tổng của cấp số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 7 trang 98 SGK Toán 11 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Vệ tinh A lần lượt truyền một tin đến vệ tinh B cho đến khi vệ tinh B phản hồi là đã nhận được.
Đề bài
Vệ tinh A lần lượt truyền một tin đến vệ tinh B cho đến khi vệ tinh B phản hồi là đã nhận được. Biết khả năng vệ tinh B phản hồi đã nhận được tin ở mỗi lần A gửi là độc lập với nhau và xác suất phản hồi mỗi lần đều là 0,4. Sử dụng sơ đồ hình cây, tính xác suất vệ tinh A phải gửi tin không quá 3 lần.
Phương pháp giải - Xem chi tiết
Sử dụng sơ đồ hình cây.
Lời giải chi tiết
Do các lần gửi tin độc lập nên ta có sơ đồ hình cây như sau:
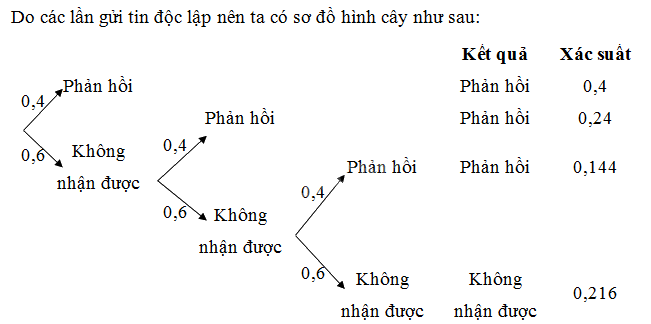
Theo sơ đồ trên thì:
Xác suất vệ tinh A phải gửi tin không quá 3 lần là:
\(0,4 + 0,24 + 0,144 = 0,784\)
Bài 7 trang 98 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về cấp số cho và cấp số nhân. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Để tìm số hạng tổng quát của cấp số cho, ta cần xác định số hạng đầu (u1) và công sai (d). Từ đó, ta có thể sử dụng công thức un = u1 + (n-1)d để tìm số hạng thứ n của cấp số.
Ví dụ, nếu cấp số cho là 2, 5, 8, 11,... thì u1 = 2 và d = 3. Vậy số hạng tổng quát của cấp số này là un = 2 + (n-1)3 = 3n - 1.
Tương tự như cấp số cho, để tìm số hạng tổng quát của cấp số nhân, ta cần xác định số hạng đầu (u1) và công bội (q). Sau đó, ta sử dụng công thức un = u1 * q(n-1) để tìm số hạng thứ n của cấp số.
Ví dụ, nếu cấp số nhân là 3, 6, 12, 24,... thì u1 = 3 và q = 2. Vậy số hạng tổng quát của cấp số này là un = 3 * 2(n-1).
Tổng của n số hạng đầu của cấp số cho được tính theo công thức Sn = (n/2) * (u1 + un) hoặc Sn = (n/2) * [2u1 + (n-1)d].
Ví dụ, để tính tổng của 10 số hạng đầu của cấp số 2, 5, 8, 11,... ta có thể sử dụng công thức S10 = (10/2) * [2*2 + (10-1)*3] = 5 * (4 + 27) = 5 * 31 = 155.
Tổng của n số hạng đầu của cấp số nhân được tính theo công thức Sn = u1 * (1 - qn) / (1 - q) (với q ≠ 1).
Ví dụ, để tính tổng của 5 số hạng đầu của cấp số nhân 3, 6, 12, 24,... ta có thể sử dụng công thức S5 = 3 * (1 - 25) / (1 - 2) = 3 * (1 - 32) / (-1) = 3 * (-31) / (-1) = 93.
Để luyện tập thêm, các em có thể giải các bài tập tương tự trong SGK Toán 11 tập 2 – Chân trời sáng tạo hoặc tìm kiếm trên các trang web học toán online.
Bài 7 trang 98 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về cấp số cho và cấp số nhân. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ tự tin giải bài tập này và các bài tập tương tự.