Bài 6 trang 34 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Cấp số cho và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán liên quan đến cấp số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Hình nào vẽ đồ thị của hàm số (y = {log _{frac{1}{2}}}x)?
Đề bài
Hình nào vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\)?
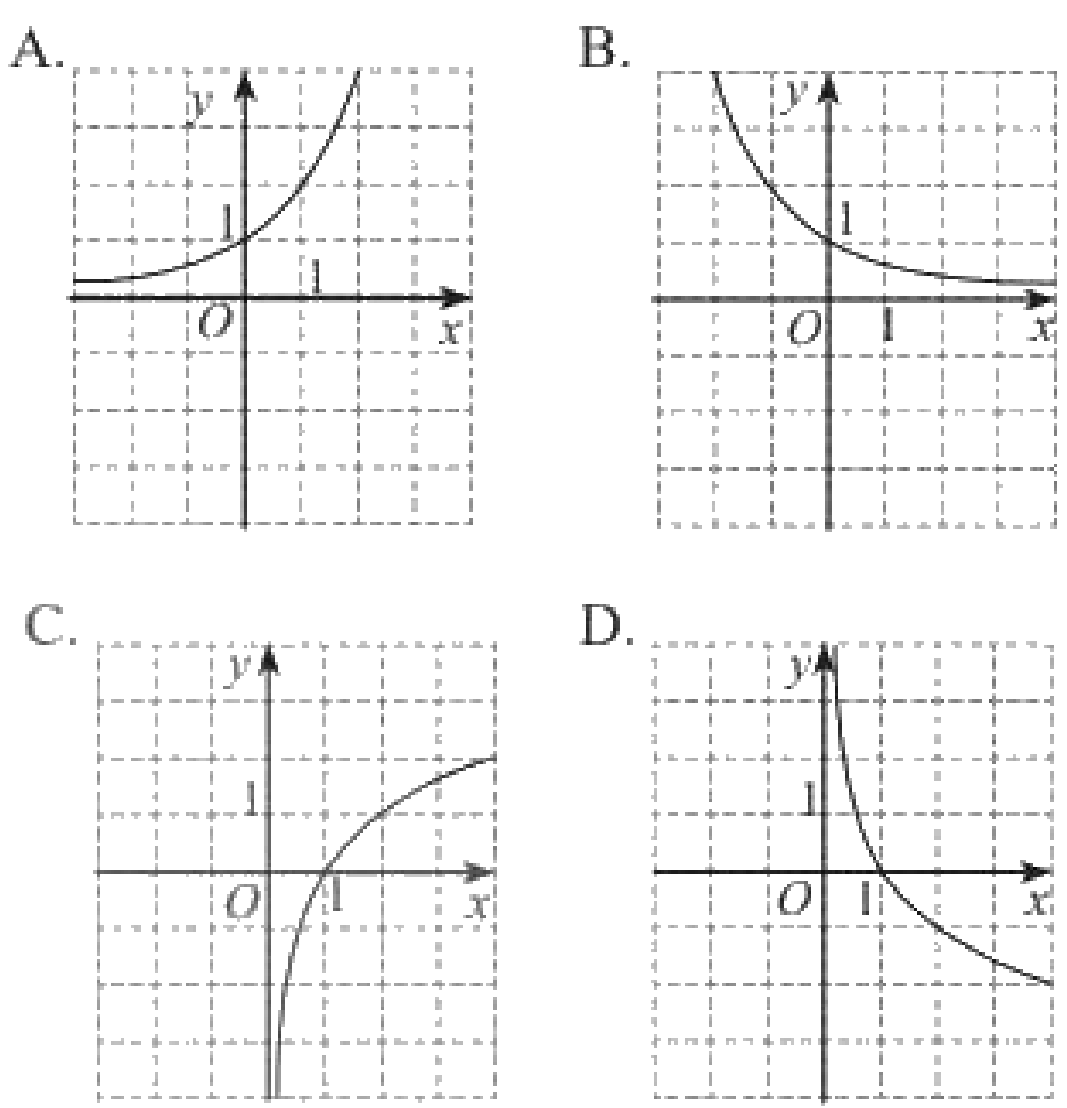
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của đồ thị hàm số \(y = {\log _a}x\).
Lời giải chi tiết
‒ Hàm số \(y = {\log _{\frac{1}{2}}}x\) nghịch biến trên \(\left( {0; + \infty } \right)\). Loại A, C.
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x = + \infty \). Loại B.
Chọn D.
Bài 6 trang 34 SGK Toán 11 tập 2 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về cấp số cho và cấp số nhân. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài tập yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Ví dụ 1: Cho cấp số cho có số hạng đầu u1 = 2 và công sai d = 3. Tìm số hạng thứ 5 của cấp số.
Lời giải: Số hạng thứ 5 của cấp số là u5 = u1 + (5-1)d = 2 + 4*3 = 14.
Ví dụ 2: Cho cấp số nhân có số hạng đầu u1 = 1 và công bội q = 2. Tính tổng của 5 số hạng đầu tiên của cấp số.
Lời giải: Tổng của 5 số hạng đầu tiên của cấp số là S5 = u1(q5 - 1)/(q - 1) = 1*(25 - 1)/(2 - 1) = 31.
Khi giải bài tập về cấp số, học sinh nên thực hiện theo các bước sau:
Các dạng bài tập thường gặp về cấp số bao gồm:
Để nắm vững kiến thức về cấp số, học sinh nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. giaitoan.edu.vn cung cấp nhiều bài tập luyện tập với các mức độ khó khác nhau, giúp học sinh rèn luyện kỹ năng giải toán hiệu quả.
Bài 6 trang 34 SGK Toán 11 tập 2 - Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức về cấp số cho và cấp số nhân. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, học sinh sẽ nắm vững kiến thức và giải bài tập một cách hiệu quả.
Việc hiểu rõ các khái niệm và công thức liên quan đến cấp số là rất quan trọng để giải quyết các bài toán thực tế. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất trong môn Toán 11.
Ngoài ra, học sinh có thể tham khảo thêm các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải toán.