Chào mừng bạn đến với bài học về Lý thuyết Giá trị lượng giác của một góc lượng giác, một phần quan trọng trong chương trình Toán 11 Chân trời sáng tạo.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về giá trị lượng giác, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
1. Giá trị lượng giác của góc lượng giác
1. Giá trị lượng giác của góc lượng giác
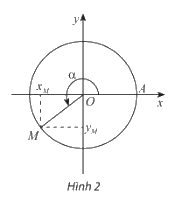
- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
- Các giá trị sin\(\alpha \), cos\(\alpha \), tan\(\alpha \), cot\(\alpha \) được gọi là các giá trị lượng giác của góc lượng giác \(\alpha \).
*Chú ý:
a, Trục tung là trục sin, trục hoành là trục côsin.
Trục As có gốc ở điểm A(1;0) và song song với trục sin là trục tang.
Trục Bt có gốc ở điểm B(0;1) và song song với trục coossin gọi là trục côtang.
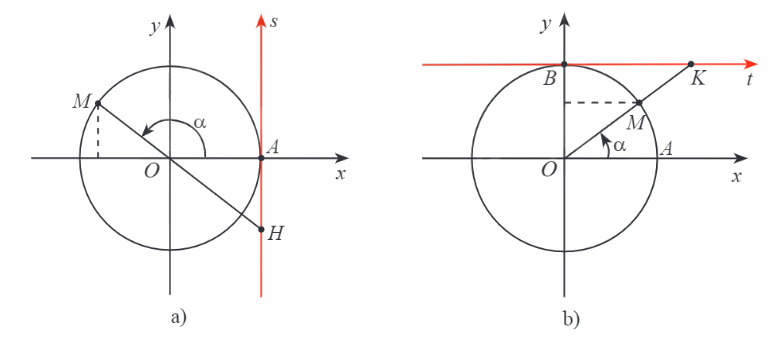
b, \(\sin \alpha \)và \(\cos \alpha \) xác định với mọi \(\alpha \in \mathbb{R}\).
\(\tan \alpha \)xác định với các góc \(\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
\(\cot \alpha \) xác định với các góc \(\alpha \ne k\pi ,k \in \mathbb{Z}\).
c, Với mọi góc lượng giác \(\alpha \) và số nguyên k, ta có:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha + k\pi } \right) = \cot \alpha \end{array}\)
d, Bảng các giá trị lượng giác đặc biệt
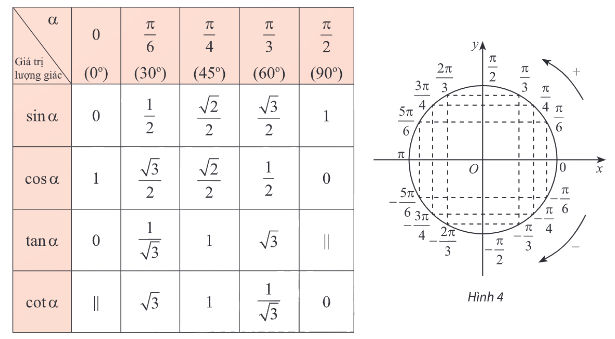
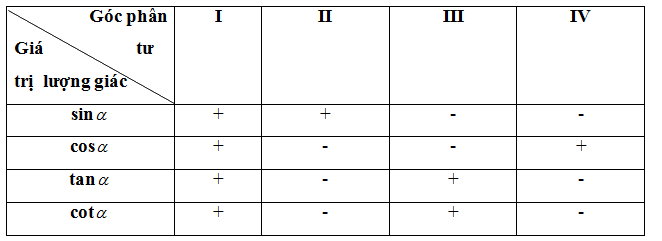
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay
- Lần lượt ấn các phím SHIFT \( \to \)MENU \( \to \)2:
Để chọn đơn vị độ: ấn phím 1 (Degree).
Để chọn đơn vị radian: ấn phím 2 (Radian).
- Ấn các phím MENU 1 để vào chế độ tính toán.
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
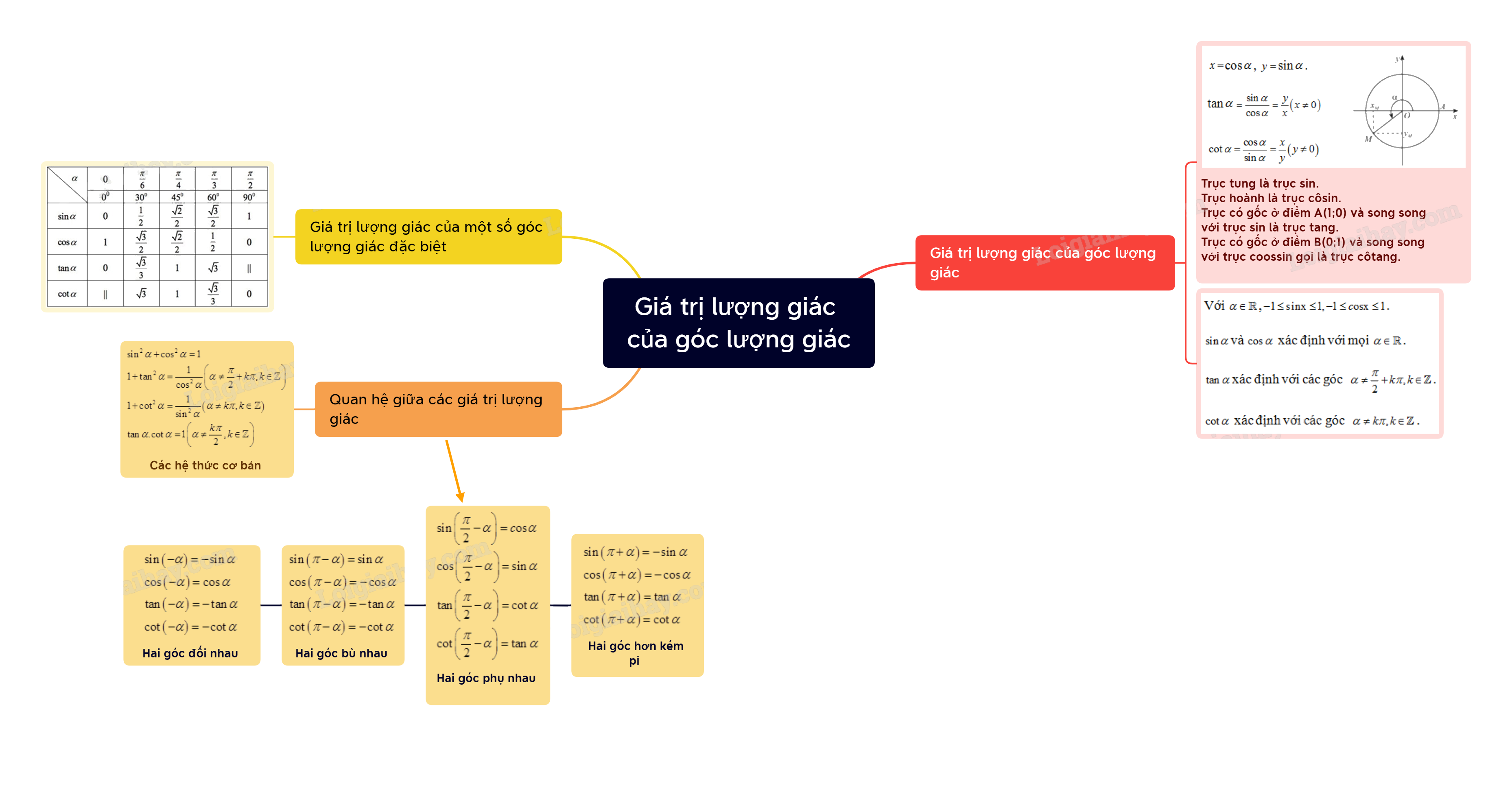
Giá trị lượng giác của một góc lượng giác là một khái niệm cơ bản và quan trọng trong toán học, đặc biệt là trong chương trình Toán 11. Hiểu rõ về giá trị lượng giác sẽ giúp học sinh giải quyết các bài toán liên quan đến tam giác, đường tròn lượng giác và các ứng dụng thực tế.
Trước khi đi sâu vào giá trị lượng giác, chúng ta cần hiểu rõ về góc lượng giác và cách đo góc. Góc lượng giác được định nghĩa là một hình tạo bởi hai tia gốc chung và một phần mặt phẳng bị giới hạn bởi hai tia đó. Số đo của góc lượng giác có thể được biểu diễn bằng độ hoặc radian.
Mối quan hệ giữa độ và radian là: 180° = π radian.
Giá trị lượng giác của một góc α (0 ≤ α ≤ 180°) được định nghĩa trên đường tròn lượng giác như sau:
Các giá trị lượng giác này có những tính chất quan trọng sau:
Việc nắm vững giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°) là rất quan trọng để giải quyết các bài toán lượng giác một cách nhanh chóng và chính xác. Dưới đây là bảng giá trị lượng giác của các góc đặc biệt:
| Góc (α) | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan α | 0 | 1/√3 | 1 | √3 | Không xác định |
| cot α | Không xác định | √3 | 1 | 1/√3 | 0 |
Ngoài các tính chất cơ bản, còn có một số công thức lượng giác quan trọng cần được ghi nhớ:
Giá trị lượng giác có rất nhiều ứng dụng trong thực tế, bao gồm:
Để củng cố kiến thức về giá trị lượng giác, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Giá trị lượng giác của một góc lượng giác. Chúc bạn học tập tốt!