Bài 10 trang 87 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến đạo hàm của hàm số. Bài tập này giúp học sinh củng cố kiến thức về quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 10 trang 87, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Gọi \(M,N,P\) lần lượt là trung điểm của \(SB,SC\) và \(SD\). Tính khoảng cách giữa \(AM\) và \(NP\).
Phương pháp giải - Xem chi tiết
Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
Lời giải chi tiết
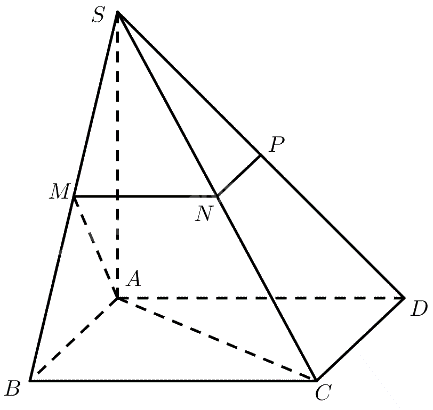
\(M\) là trung điểm của \(SB\)
\(N\) là trung điểm của \(SC\)
\( \Rightarrow MN\) là đường trung bình của \(\Delta SBC\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel BC\\BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow MN \bot C{\rm{D}}\)
Mà \(C{\rm{D}}\parallel NP\) \( \Rightarrow MN \bot NP\) (1)
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right)\)
Mà \(MN\parallel BC\)\( \Rightarrow MN \bot \left( {SAB} \right) \Rightarrow MN \bot AM\)(2)
Từ (1) và (2) \( \Rightarrow d\left( {AM,NP} \right) = MN = \frac{1}{2}BC = \frac{a}{2}\).
Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và các quy tắc tính đạo hàm. Dưới đây là giải chi tiết từng phần của bài tập này:
(Nội dung đề bài Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo được trình bày đầy đủ tại đây)
Để giải bài tập này, chúng ta cần áp dụng các kiến thức sau:
Bước 1: Tính đạo hàm của hàm số f(x).
(Giải thích chi tiết cách tính đạo hàm f'(x) với các bước rõ ràng, sử dụng công thức đạo hàm phù hợp)
Bước 2: Tìm các điểm tới hạn của hàm số.
(Giải thích cách tìm các điểm x sao cho f'(x) = 0 hoặc f'(x) không xác định)
Bước 3: Lập bảng biến thiên của hàm số.
(Hướng dẫn cách lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số)
Bước 4: Kết luận.
(Đưa ra kết luận về tính đơn điệu, cực trị của hàm số dựa trên bảng biến thiên)
Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng xem xét một ví dụ minh họa:
(Trình bày một ví dụ tương tự Bài 10 trang 87, giải chi tiết từng bước và giải thích rõ ràng)
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập sau:
Lưu ý:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
Các chủ đề liên quan: