Chào mừng bạn đến với bài học về Lý thuyết Đạo hàm trong chương trình Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn. Đạo hàm là một khái niệm nền tảng quan trọng trong giải tích, giúp chúng ta hiểu rõ hơn về sự thay đổi của hàm số.
Bài học này sẽ cung cấp cho bạn kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
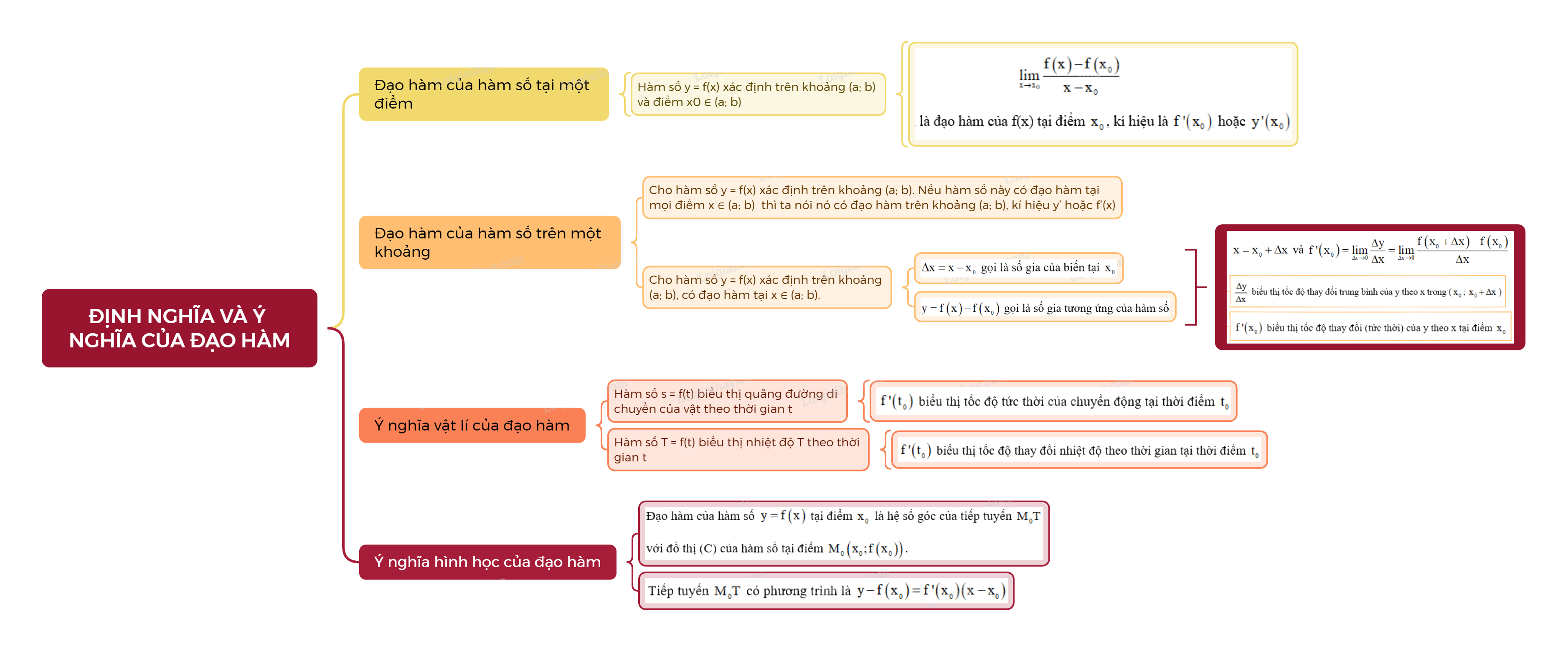
1. Đạo hàm Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\).
1. Đạo hàm
Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\).
Nếu tồn tại giới hạn (hữu hạn)
\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\)
thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm \({x_0}\), kí hiệu là \(f'\left( {{x_0}} \right)\) hoặc \(y'\left( {{x_0}} \right)\).
Vậy:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
Chú ý:
- Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu hàm số này có đạo hàm tại mọi điểm \(x \in \left( {a;b} \right)\) thì ta nói nó có đạo hàm trên khoảng (a; b), kí hiệu y’ hoặc f’(x).
- Cho hàm số y = f(x) xác định trên khoảng (a; b), có đạo hàm tại \({x_0} \in \left( {a;b} \right)\).
a) Đại lượng \(\Delta x = x - {x_0}\) gọi là số gia của biến tại \({x_0}\). Đại lượng \(y = f\left( x \right) - f\left( {{x_0}} \right)\) gọi là số gia tương ứng của hàm số. Khi đó, \(x = {x_0} + \Delta x\) và
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)}}{{\Delta x}}\).
b) Tỉ số \(\frac{{\Delta y}}{{\Delta x}}\) biểu thị tốc độ thay đổi trung bình của đại lượng y theo đại lượng x trong khoảng từ \({x_0}\) đến \({x_0} + \Delta x\); còn \(f'\left( {{x_0}} \right)\) biểu thị tốc độ thay đổi (tức thời) của đại lượng y theo đại lượng x tại điểm \({x_0}\).
2. Ý nghĩa vật lí của đạo hàm
- Nếu hàm số s = f(t) biểu thị quãng đường di chuyển của vật theo thời gian t thì \(f'\left( {{t_0}} \right)\) biểu thị tốc độ tức thời của chuyển động tại thời điểm \({t_0}\).
- Nếu hàm số T = f(t) biểu thị nhiệt độ T theo thời gian t thì \(f'\left( {{t_0}} \right)\) biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm \({t_0}\).
3. Ý nghĩa hình học của đạo hàm
Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) là hệ số góc của tiếp tuyến \({M_0}T\) với đồ thị (C) của hàm số tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\).
Tiếp tuyến \({M_0}T\) có phương trình là \(y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
Đạo hàm là một khái niệm then chốt trong chương trình Toán 11, đặc biệt là với bộ sách Chân Trời Sáng Tạo. Nó không chỉ là công cụ để giải quyết các bài toán liên quan đến sự thay đổi của hàm số mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Đạo hàm của một hàm số f(x) tại một điểm x0, ký hiệu là f'(x0), biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó. Về mặt hình học, đạo hàm là hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm x0.
Công thức tính đạo hàm theo định nghĩa:
f'(x0) = limΔx→0 [f(x0 + Δx) - f(x0)] / Δx
Để đơn giản hóa việc tính đạo hàm, chúng ta sử dụng các quy tắc sau:
Dưới đây là đạo hàm của một số hàm số cơ bản thường gặp:
| Hàm số f(x) | Đạo hàm f'(x) |
|---|---|
| C (hằng số) | 0 |
| x | 1 |
| xn | nxn-1 |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| ex | ex |
| ln(x) | 1/x |
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Khi tính đạo hàm, cần lưu ý:
Hy vọng bài học này đã giúp bạn nắm vững kiến thức về Lý thuyết Đạo hàm - Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!