Chào mừng các em học sinh đến với lời giải chi tiết Bài 4 trang 93 SGK Toán 11 tập 2 – Chân trời sáng tạo. Bài học này thuộc chương trình học Toán 11, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Một xạ thủ bắn lần lượt 2 viên đạn vào một bia. Xác suất trúng đích của viên thứ nhất và thứ hai lần lượt là 0,9 và 0,6.
Đề bài
Một xạ thủ bắn lần lượt 2 viên đạn vào một bia. Xác suất trúng đích của viên thứ nhất và thứ hai lần lượt là 0,9 và 0,6. Biết rằng kết quả các lần bắn là độc lập với nhau. Tính xác suất của các biến cố sau bằng cách sử dụng sơ đồ hình cây:
a) “Cả 2 lần bắn đều trúng đích”;
b) “Cả 2 lần bắn đều không trúng đích”;
c) “Lần bắn thứ nhất trúng đích, lần bắn thứ hai không trúng đích”.
Phương pháp giải - Xem chi tiết
Sử dụng sơ đồ hình cây.
Lời giải chi tiết
Do hai lần bắn độc lập nên ta có sơ đồ hình cây như sau:
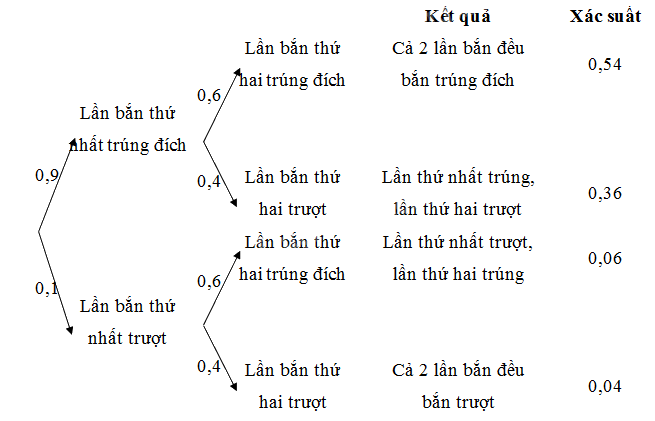
Theo sơ đồ trên thì:
a) Xác suất cả 2 lần bắn đều trúng đích là 0,54.
b) Xác suất cả 2 lần bắn đều không trúng đích là 0,04.
c) Xác suất lần bắn thứ nhất trúng đích, lần bắn thứ hai không trúng đích là 0,36.
Bài 4 trang 93 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của Bài 4 trang 93 SGK Toán 11 tập 2 – Chân trời sáng tạo:
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = f(x) = x^3 - 3x^2 + 2. Tìm các điểm cực trị của hàm số.)
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Bước 1: Tính đạo hàm bậc nhất
Ta có hàm số y = f(x) = x^3 - 3x^2 + 2. Áp dụng quy tắc tính đạo hàm của tổng và lũy thừa, ta được:
f'(x) = 3x^2 - 6x
Bước 2: Tìm các điểm mà f'(x) = 0 hoặc không xác địnhĐể tìm các điểm mà f'(x) = 0, ta giải phương trình:
3x^2 - 6x = 0
⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
Đạo hàm f'(x) xác định với mọi x thuộc R.
Bước 3: Xác định dấu của f'(x) trên các khoảng xác địnhTa xét các khoảng sau:
Dựa vào bảng xét dấu của f'(x), ta có:
Vậy hàm số y = f(x) = x^3 - 3x^2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Để hiểu sâu hơn về ứng dụng của đạo hàm trong việc giải quyết các bài toán cực trị, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 11 tập 2 và các tài liệu ôn tập khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Ngoài ra, các em cũng có thể tìm hiểu thêm về các ứng dụng khác của đạo hàm trong các lĩnh vực khoa học và kỹ thuật.
Lưu ý: Đây chỉ là một ví dụ minh họa cho cách giải Bài 4 trang 93 SGK Toán 11 tập 2 – Chân trời sáng tạo. Tùy thuộc vào đề bài cụ thể, các em cần áp dụng các quy tắc và phương pháp giải phù hợp.