Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 122, 123, 124 sách giáo khoa Toán 11 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Trong Hình 4, xét phép chiếu theo phương (l) lên mặt phẳng (left( P right)), mặt phẳng (left( Q right)) chứa đường thẳng (a) và song song với phương chiếu
Trong Hình 4, xét phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa đường thẳng \(a\) và song song với phương chiếu.
a) Khi điểm \(M\) thay đổi trên đường thẳng \(a\) thì ảnh \(M'\) của nó thay đổi ở đâu?
b) Từ đó hãy chỉ ra ảnh của đường thẳng \(a\) qua phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\).
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Khi điểm \(M\) thay đổi trên đường thẳng \(a\) thì ảnh \(M'\) của nó thay đổi trên đường thẳng \(a'\).
b) Ảnh của đường thẳng \(a\) qua phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\) là đường thẳng \(a'\).
Trong Hình 5, xét phép chiếu theo phương \(l\) với mặt phẳng chiếu \(\left( P \right)\). Biết \(a\parallel b\) với \(a \subset \left( Q \right)\) và \(b \subset \left( R \right)\). Nêu nhận xét về vị trí tương đối của hình chiếu \(a',b'\) của \(a,b\) trong hai trường hợp: \(\left( Q \right)\parallel \left( R \right);\left( Q \right) \equiv \left( R \right)\).

Phương pháp giải:
‒ Quan sát hình ảnh và trả lời câu hỏi.
‒ Sử dụng định lí: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
Lời giải chi tiết:
Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'\)
Vậy nếu \(\left( Q \right)\parallel \left( R \right)\) thì \(a'\parallel b'\); nếu \(\left( Q \right) \equiv \left( R \right)\) thì \(a' \equiv b'\).
Cho hình thang \(ABCD\) có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\). Chứng minh rằng \(A'B'C'D'\) cũng là một hình thang và \(A'B' = 2C'D'\).
Phương pháp giải:
Sử dụng tính chất của phép chiếu song song:
‒ Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau.
‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
\(ABCD\) là hình thang có đáy lớn \(AB \Rightarrow AB\parallel CD\).
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\) nên \(A'B'\parallel C'D'\). Vậy \(A'B'C'D'\) cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà \(AB = 2CD,AB\parallel CD\) và \(A'B'\parallel C'D'\) nên \(A'B' = 2C'D'\).
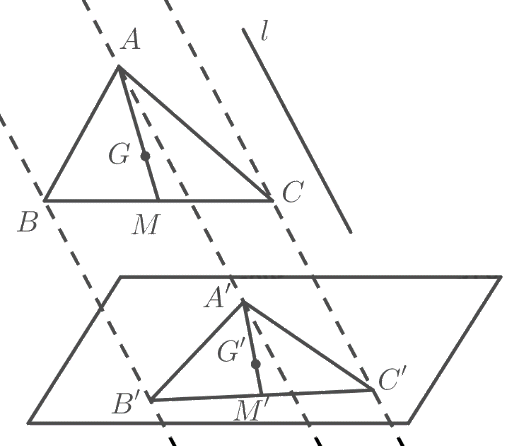
Cho \(G\) là trọng tâm tam giác \(ABC\), \(M\) là trung điểm \(BC\) và hình chiếu song song của tam giác \(ABC\) là tam giác \(A'B'C'\). Chứng minh rằng hình chiếu \(M'\) của \(M\) là trung điểm của \(B'C'\) và hình chiếu \(G'\) của \(G\) cũng là trọng tâm tam giác \(A'B'C'\).
Phương pháp giải:
Sử dụng tính chất của phép chiếu song song:
‒ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:

Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).
Mục 2 của SGK Toán 11 tập 1 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào phân tích từng bài tập, cung cấp lời giải chi tiết và giải thích rõ ràng các bước thực hiện.
Thông thường, Mục 2 sẽ bao gồm các nội dung sau:
Bài 1: (Nêu đề bài tập và giải chi tiết từng bước). Ví dụ: Bài 1 yêu cầu tính giá trị của biểu thức. Lời giải sẽ bao gồm các bước biến đổi biểu thức, áp dụng công thức và tính toán kết quả cuối cùng. Giải thích rõ ràng lý do tại sao lại thực hiện từng bước như vậy.
Bài 2: (Nêu đề bài tập và giải chi tiết từng bước). Ví dụ: Bài 2 yêu cầu chứng minh một đẳng thức. Lời giải sẽ bao gồm các bước biến đổi đẳng thức, sử dụng các công thức và định lý đã học để chứng minh đẳng thức đúng.
Bài 3: (Nêu đề bài tập và giải chi tiết từng bước).
Bài 4: (Nêu đề bài tập và giải chi tiết từng bước).
Bài 5: (Nêu đề bài tập và giải chi tiết từng bước).
Bài 6: (Nêu đề bài tập và giải chi tiết từng bước).
Bài 7: (Nêu đề bài tập và giải chi tiết từng bước).
Bài 8: (Nêu đề bài tập và giải chi tiết từng bước).
Bài 9: (Nêu đề bài tập và giải chi tiết từng bước).
Để giải bài tập Toán 11 tập 1 chương trình Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Kiến thức và kỹ năng được học trong Mục 2 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của Toán học và các môn khoa học khác. Ví dụ, kiến thức về hàm số được sử dụng trong Vật lý để mô tả các hiện tượng tự nhiên, trong Kinh tế để phân tích thị trường và dự báo xu hướng.
Ngoài SGK Toán 11 tập 1 chương trình Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng bài viết này sẽ giúp các em học sinh giải quyết thành công các bài tập trong mục 2 trang 122, 123, 124 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!