Chào mừng các em học sinh đến với lời giải chi tiết Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo. Bài học này thuộc chương trình đại số lớp 11, tập trung vào các kiến thức về hàm số và đồ thị hàm số.
giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
Đề bài
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a) \(\frac{{ - 17\pi }}{3}\)
b) \(\frac{{13\pi }}{4}\)
c) \( - 765^\circ \)
Phương pháp giải - Xem chi tiết
Biểu diễn dựa trên các góc đặc biệt
Lời giải chi tiết
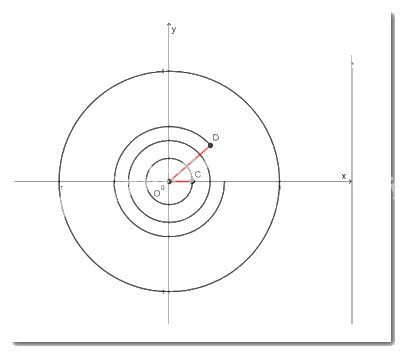
a) \(\frac{{ - 17\pi }}{3} = - 5\pi - \frac{{2\pi }}{3}\)
\( \Rightarrow \left( {OC,OD} \right) = \frac{{ - 17\pi }}{3}\)
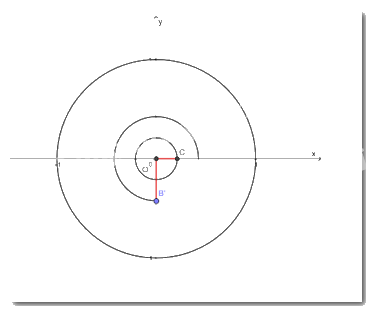
b) \(\frac{{13\pi }}{4} = 3\pi + \frac{\pi }{4}\)
\( \Rightarrow \left( {OC,OB'} \right) = \frac{{13\pi }}{4}\)
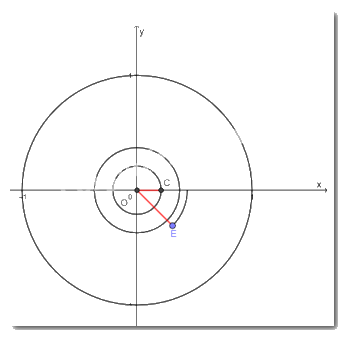
c) \( - 765^\circ = 2.\left( { - 360^\circ } \right) - 45^\circ \)
\( \Rightarrow \left( {OC;OE} \right) = - 765^\circ \)
Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để xác định tập xác định, tập giá trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm cơ bản về hàm số bậc hai, bao gồm:
Để giải Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo, các em thực hiện theo các bước sau:
Xét hàm số y = 2x2 - 4x + 1. Ta có:
Dựa vào các thông tin trên, ta có thể vẽ đồ thị hàm số y = 2x2 - 4x + 1.
Khi giải Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo, các em cần lưu ý những điều sau:
Để củng cố kiến thức về hàm số bậc hai, các em có thể làm thêm các bài tập tương tự sau:
Bài 3 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc hai và đồ thị hàm số. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ tự tin giải bài tập này một cách hiệu quả.