Bài 3 trang 64 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp (S.ABCD) có đáy là hình vuông cạnh bằng (asqrt 2 ), có các cạnh bên đều bằng (2a).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(a\sqrt 2 \), có các cạnh bên đều bằng \(2a\).
a) Tính góc giữa \(SC\) và \(AB\).
b) Tính diện tích hình chiếu vuông góc của tam giác \(SAB\) trên mặt phẳng \(\left( {ABCD} \right)\).
Phương pháp giải - Xem chi tiết
a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
b) Sử dụng phép chiếu vuông góc.
Lời giải chi tiết
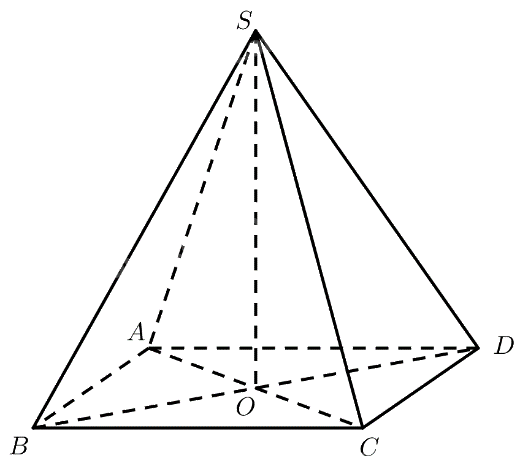
a) Ta có:
\(AB\parallel C{\rm{D}} \Rightarrow \left( {SC,AB} \right) = \left( {SC,C{\rm{D}}} \right) = \widehat {SC{\rm{D}}}\)
Xét \(\Delta SCD\) có:
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{{\rm{D}}^2} - S{{\rm{D}}^2}}}{{2.SC.C{\rm{D}}}} = \frac{{\sqrt 2 }}{4} \Rightarrow \widehat {SCD} \approx {69^ \circ }18'\)
Vậy \(\left( {SC,AB} \right) \approx {69^ \circ }18'\).
b) Gọi \(O = AC \cap B{\rm{D}}\).
\(\Delta SAC\) cân tại \(S \Rightarrow SO \bot AC\)
\(\Delta SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow O\) là hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\).
Lại có \(A,B \in \left( {ABCD} \right)\).
Vậy tam giác \(OAB\) là hình chiếu vuông góc của tam giác \(SAB\) lên mặt phẳng \(\left( {ABCD} \right)\)
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 2a\)
Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.
\(\begin{array}{l} \Rightarrow AO = BO = \frac{{AC}}{2} = a\\ \Rightarrow {S_{OAB}} = \frac{1}{2}AO.BO = \frac{1}{2}a.a = \frac{1}{2}{a^2}\end{array}\)
Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là \(\frac{1}{2}{a^2}\)
Bài 3 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 3 yêu cầu học sinh giải các bài toán liên quan đến việc tìm đạo hàm của hàm số, xác định khoảng đơn điệu của hàm số và tìm cực trị của hàm số. Cụ thể, bài tập có thể bao gồm:
Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.
Tìm khoảng đơn điệu của hàm số g(x) = x4 - 4x3 + 6x2 - 4x + 1.
Tìm cực đại và cực tiểu của hàm số h(x) = x2 - 2x + 3.
Giải bài 3a:
Để tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1, ta sử dụng quy tắc đạo hàm của tổng và hiệu, cũng như quy tắc đạo hàm của lũy thừa:
f'(x) = 3x2 - 6x + 2
Giải bài 3b:
Để tìm khoảng đơn điệu của hàm số g(x) = x4 - 4x3 + 6x2 - 4x + 1, ta thực hiện các bước sau:
Tính đạo hàm g'(x) = 4x3 - 12x2 + 12x - 4.
Giải phương trình g'(x) = 0 để tìm các điểm dừng của hàm số. Ta có: 4x3 - 12x2 + 12x - 4 = 0 ⇔ x3 - 3x2 + 3x - 1 = 0 ⇔ (x - 1)3 = 0 ⇔ x = 1.
Xét dấu của g'(x) trên các khoảng (-∞, 1) và (1, +∞). Ta thấy rằng g'(x) < 0 trên (-∞, 1) và g'(x) > 0 trên (1, +∞). Do đó, hàm số g(x) nghịch biến trên (-∞, 1) và đồng biến trên (1, +∞).
Giải bài 3c:
Để tìm cực đại và cực tiểu của hàm số h(x) = x2 - 2x + 3, ta thực hiện các bước sau:
Tính đạo hàm h'(x) = 2x - 2.
Giải phương trình h'(x) = 0 để tìm các điểm dừng của hàm số. Ta có: 2x - 2 = 0 ⇔ x = 1.
Tính đạo hàm bậc hai h''(x) = 2.
Vì h''(1) = 2 > 0, nên hàm số h(x) đạt cực tiểu tại x = 1. Giá trị cực tiểu là h(1) = 12 - 2(1) + 3 = 2.
Khi giải các bài tập về đạo hàm, học sinh cần nắm vững các quy tắc đạo hàm cơ bản, bao gồm:
Quy tắc đạo hàm của tổng và hiệu.
Quy tắc đạo hàm của tích và thương.
Quy tắc đạo hàm của hàm hợp.
Đạo hàm của các hàm số cơ bản (hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit).
Ngoài ra, học sinh cũng cần chú ý đến việc xác định đúng khoảng đơn điệu và cực trị của hàm số. Để làm được điều này, học sinh cần xét dấu của đạo hàm trên các khoảng xác định của hàm số.
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Tìm vận tốc và gia tốc của một vật chuyển động.
Tìm tốc độ thay đổi của một đại lượng nào đó.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của một hàm số.
Giải các bài toán tối ưu hóa.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập Bài 3 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo, các em học sinh sẽ hiểu rõ hơn về kiến thức đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế.