Bài 5 trang 70 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến phép biến hóa affine. Bài tập này giúp học sinh củng cố kiến thức về phép biến hóa affine, ma trận biểu diễn của phép biến hóa affine và ứng dụng của chúng trong hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5 trang 70, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Đề bài
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông \({H_0}\) cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông \({H_0}\) thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình \({H_1}\) (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của \({H_1}\) thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình \({H_2}\) (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình \({H_n}\left( {n = 1,2,3,...} \right)\).
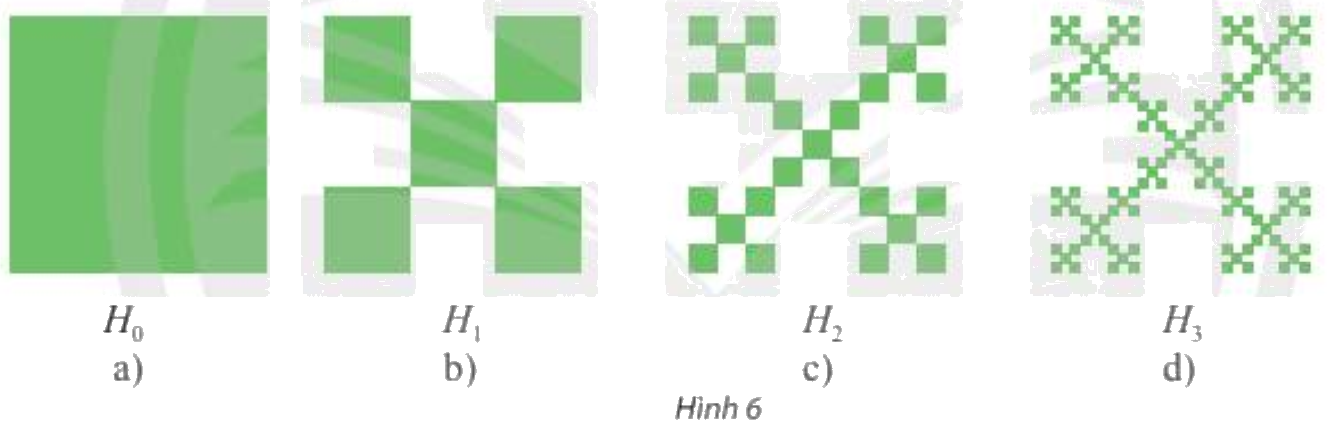
Ta có: \({H_1}\) có 5 hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}\);
\({H_2}\) có \(5.5 = {5^2}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}\);…
Từ đó, nhận được hình \({H_n}\) có \({5^n}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{{{3^n}}}\).
a) Tính diện tích \({S_n}\) của \({H_n}\) và tính \(\lim {S_n}\).
b) Tính chu vi \({p_n}\) của \({H_n}\) và tính \(\lim {p_n}\).
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích \(\lim {S_n}\) và chu vi \(\lim {p_n}\)).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) và công thức tính giới hạn cơ bản: \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\).
Lời giải chi tiết
a) Ta có:
Diện tích \({H_1}\) bằng \(5.{\left( {\frac{1}{3}} \right)^2}\);
Diện tích \({H_2}\) bằng \({5^2}.{\left( {{{\left( {\frac{1}{3}} \right)}^2}} \right)^2} = {5^2}.{\left( {\frac{1}{{{3^2}}}} \right)^2}\);
Diện tích \({H_3}\) bằng \({5^3}.{\left( {{{\left( {\frac{1}{3}} \right)}^3}} \right)^2} = {5^3}.{\left( {\frac{1}{{{3^3}}}} \right)^2}\);
…
Diện tích \({H_n}\) bằng \({5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2}\).
\({S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,...\)
\(\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0\)
b) Ta có:
Chu vi \({H_1}\) bằng \(5.4.\frac{1}{3} = 4.\frac{5}{3}\);
Chu vi \({H_2}\) bằng \({5^2}.4.{\left( {\frac{1}{3}} \right)^2} = 4.{\left( {\frac{5}{3}} \right)^2}\);
…
Chu vi \({H_n}\) bằng \({5^n}.4.{\left( {\frac{1}{3}} \right)^n} = 4.{\left( {\frac{5}{3}} \right)^n}\).
\({p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,...\)
\(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)\)
Vì \(\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} = \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0\) và \(4.{\left( {\frac{5}{3}} \right)^n} > 0\) với mọi \(n\) nên \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty \).
Bài 5 trang 70 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh hiểu sâu hơn về phép biến hóa affine và ứng dụng của nó. Dưới đây là giải chi tiết từng phần của bài tập này:
Phép biến hóa affine là một phép biến đổi hình học bảo toàn tính thẳng hàng và tỷ lệ khoảng cách giữa các điểm. Một phép biến hóa affine có thể được biểu diễn bằng một ma trận affine.
Ma trận biểu diễn của một phép biến hóa affine là một ma trận vuông cấp 3, có dạng:
A = [[a, b, c], [d, e, f], [g, h, i]]
Trong đó, a, b, c, d, e, f, g, h, i là các số thực.
Bài 5a: Cho hai điểm A(1; 2) và B(3; 4). Tìm ảnh của A và B qua phép biến hóa affine f(x; y) = (2x + y; x - y).
Giải:
Bài 5b: Tìm ma trận biểu diễn của phép biến hóa affine f(x; y) = (2x + y; x - y).
Giải:
Ma trận biểu diễn của phép biến hóa affine f(x; y) = (2x + y; x - y) là:
A = [[2, 1, 0], [1, -1, 0], [0, 0, 1]]
Phép biến hóa affine có nhiều ứng dụng trong hình học, đồ họa máy tính và các lĩnh vực khác. Ví dụ, phép biến hóa affine có thể được sử dụng để:
Để củng cố kiến thức về phép biến hóa affine, các em có thể tự giải thêm các bài tập sau:
Bài 5 trang 70 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về phép biến hóa affine và ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!