Chào mừng bạn đến với bài học về lý thuyết các quy tắc tính đạo hàm trong chương trình Toán 11 Chân trời sáng tạo. Đây là một phần kiến thức quan trọng, nền tảng cho việc giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong các lĩnh vực khác.
Bài học này sẽ cung cấp cho bạn một cái nhìn tổng quan về các quy tắc tính đạo hàm cơ bản, cùng với các ví dụ minh họa cụ thể để bạn dễ dàng nắm bắt và áp dụng vào thực tế.
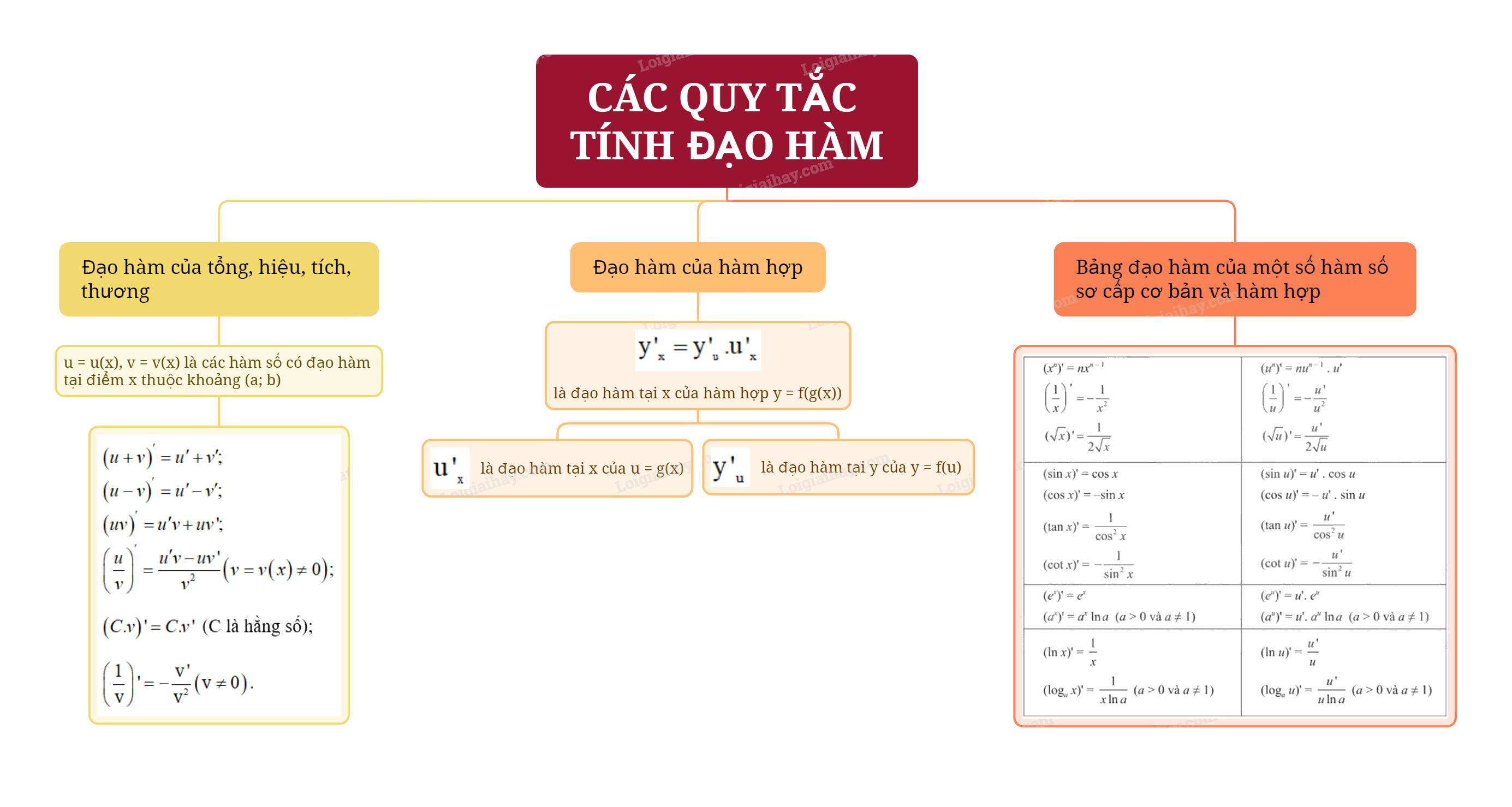
1. Đạo hàm của tổng, hiệu, tích, thương Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc tập xác định.
1. Đạo hàm của tổng, hiệu, tích, thương
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc tập xác định. Khi đó
\(\begin{array}{*{20}{l}}{{{\left( {u + v} \right)}^\prime } = u' + v';}\\{{{\left( {u - v} \right)}^\prime } = u' - v';}\\{{{\left( {uv} \right)}^\prime } = u'v + uv';}\\{{{\left( {\frac{u}{v}} \right)}^\prime } = \frac{{u'v - uv'}}{{{v^2}}}\left( {v = v\left( x \right) \ne 0} \right);}\end{array}\)
\(\left( {C.v} \right)' = C.v'\) (C là hằng số);
\(\left( {\frac{1}{v}} \right)' = - \frac{{v'}}{{{v^2}}}\left( {v \ne 0} \right)\).
2. Đạo hàm của hàm hợp
Nếu hàm số u = g(x) có đạo hàm tại x là \(u{'_x}\) và hàm số y = f(u) có đạo hàm tại y là \(y{'_u}\) thì hàm hợp y = f(g(x)) có đạo hàm tại x là \(y{'_x} = y{'_u}.u{'_x}\).
3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp

4. Đạo hàm cấp hai
Cho hàm số y = f(x) có đạo hàm tại mọi điểm \(x \in \left( {a;b} \right)\) thì ta có hàm số \(y' = f'\left( x \right)\) xác định trên (a; b).
Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).
\(f''\left( x \right) = \left( {f'\left( x \right)} \right)'\).
Ý nghĩa cơ học của đạo hàm cấp hai
Đạo hàm cấp hai f”(t) là gia tốc tức thời tại thời điểm t của vân chuyển động có phương trình \(s = f\left( t \right)\).
Đạo hàm là một khái niệm cơ bản trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự thay đổi của hàm số. Trong chương trình Toán 11 Chân trời sáng tạo, học sinh sẽ được làm quen với các quy tắc tính đạo hàm, giúp đơn giản hóa quá trình tìm đạo hàm của các hàm số phức tạp.
Trước khi đi vào các quy tắc, chúng ta cần nắm vững đạo hàm của một số hàm số cơ bản:
Để tính đạo hàm của các hàm số phức tạp, chúng ta sử dụng các quy tắc sau:
Cho hai hàm số u(x) và v(x) có đạo hàm tại x:
Cho hàm số y = f(g(x)). Đạo hàm của y được tính theo công thức:
y' = f'(g(x)) * g'(x)
Ví dụ 1: Tính đạo hàm của hàm số y = 3x2 + 2x - 1
Giải:
y' = (3x2)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2
Ví dụ 2: Tính đạo hàm của hàm số y = sin(2x)
Giải:
Đặt u = 2x, khi đó y = sin(u). Ta có u' = 2 và (sin u)' = cos u. Áp dụng quy tắc hàm hợp:
y' = (sin u)' * u' = cos(2x) * 2 = 2cos(2x)
Hãy tự giải các bài tập sau để củng cố kiến thức:
Khi tính đạo hàm, cần chú ý đến thứ tự thực hiện các phép toán và áp dụng đúng các quy tắc. Việc hiểu rõ bản chất của đạo hàm và các quy tắc sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và chính xác.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết các quy tắc tính đạo hàm trong chương trình Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!