Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 22, 23, 24 sách giáo khoa Toán 11 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho (s) và (t) là hai đại lượng liên hệ với nhau theo công thức (s = {2^t}).
Cho \(s\) và \(t\) là hai đại lượng liên hệ với nhau theo công thức \(s = {2^t}\).
a) Với mỗi giá trị của \(t\) nhận giá trị trong \(\mathbb{R}\), tìm được bao nhiêu giá trị tương ứng của \(s\)? Tại sao?
b) Với mỗi giá trị của \(s\) thuộc \(\left( {0; + \infty } \right)\), có bao nhiêu giá trị tương ứng của \(t\)?
c) Viết công thức biểu thị \(t\) theo \(s\) và hoàn thành bảng sau.
Phương pháp giải:
Sử dụng khái niệm hàm số, định nghĩa lôgarit.
Lời giải chi tiết:
a) Với mỗi giá trị của \(t\) thuộc \(\mathbb{R}\), tìm được duy nhất một giá trị tương ứng của \(s\).
b) Với mỗi giá trị của \(s\) thuộc \(\left( {0; + \infty } \right)\), có duy nhất một giá trị tương ứng của \(t\).
c) \(s = {2^t} \Leftrightarrow t = {\log _2}s\)
Ta có:
a) Xét hàm số \(y = {\log _2}x\) với tập xác định \(D = \left( {0; + \infty } \right)\).

i) Hoàn thành bảng giá trị sau:

ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{{\log }_2}x} \right)\) với \(x > 0\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to {0^ + }\) và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\). Từ đó, nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to {0^ + }\) và tập giá trị của hàm số này.
Phương pháp giải:
a) Thay các giá trị của \(x\) vào hàm số sau đó dựa vào đồ thị nhận xét.
b) Lập bảng giá trị, vẽ đồ thị hàm số, sau đó dựa vào đồ thị nhận xét.
Lời giải chi tiết:
a) i)
ii) ‒ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).
‒ Hàm số đồng biến trên \(\left( {0; + \infty } \right)\).
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\log _2}x = + \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x = - \infty \).
‒ Tập giá trị: \(\mathbb{R}\).
b) Bảng giá trị:
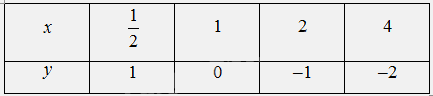
Đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\):
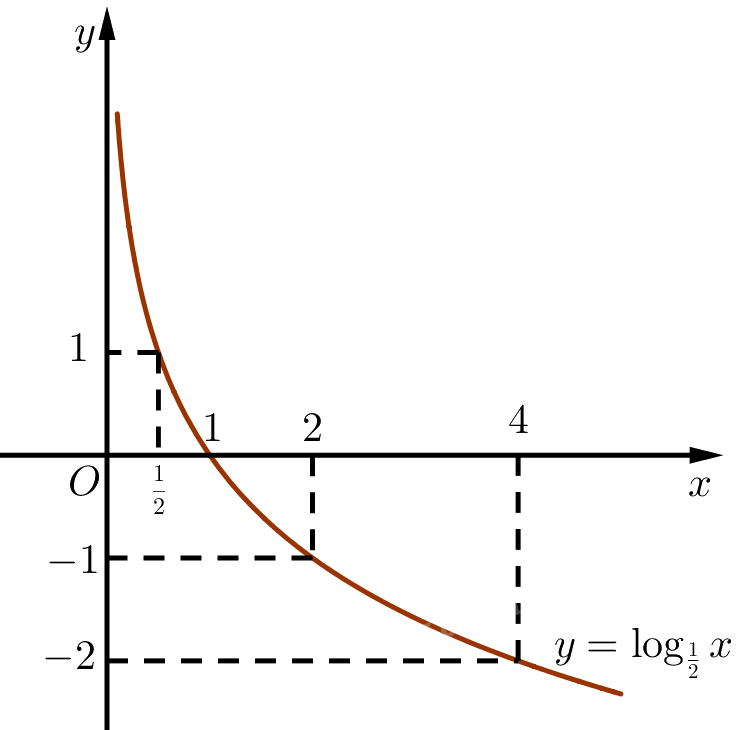
‒ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).
‒ Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x = + \infty \).
‒ Tập giá trị: \(\mathbb{R}\).
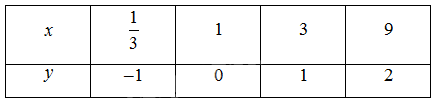
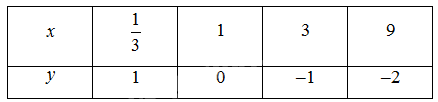
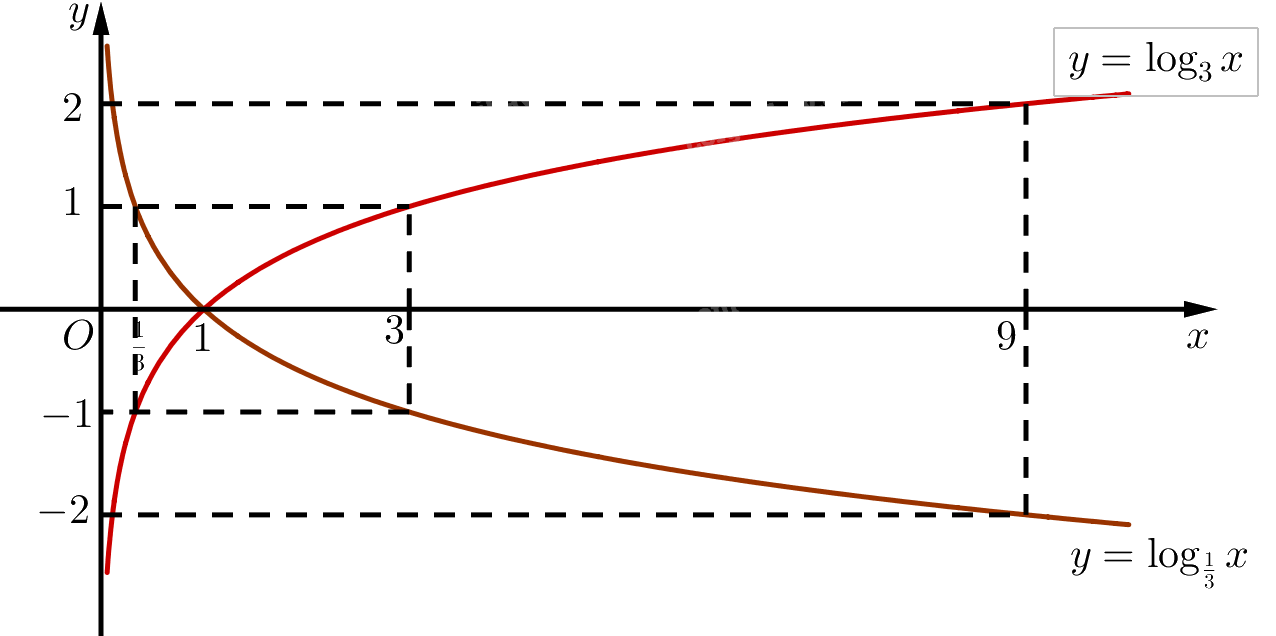
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số \(y = {\log _3}x\) và \(y = {\log _{\frac{1}{3}}}x\).
Phương pháp giải:
Lập bảng giá trị, dựa vào bảng giá trị vẽ đồ thị.
Lời giải chi tiết:
Bảng giá trị:
‒ Hàm số \(y = {\log _3}x\):

‒ Hàm số \(y = {\log _{\frac{1}{3}}}x\):

‒ Đồ thị:

So sánh các cặp số sau:
a) \({\log _{\frac{1}{2}}}4,8\) và \({\log _{\frac{1}{2}}}5,2\);
b) \({\log _{\sqrt 5 }}2\) và \({\log _5}2\sqrt 2 \);
c) \( - {\log _{\frac{1}{4}}}2\) và \({\log _{\frac{1}{2}}}0,4\).
Phương pháp giải:
Sử dụng tính chất của hàm số lôgarit.
Lời giải chi tiết:
a) Hàm số \(y = {\log _{\frac{1}{2}}}x\) có cơ số \(\frac{1}{2} < 1\) nên nghịch biến trên \(\left( {0; + \infty } \right)\).
Mà \(4,8 < 5,2\) nên \({\log _{\frac{1}{2}}}4,8 > {\log _{\frac{1}{2}}}5,2\).
b) \({\log _{\sqrt 5 }}2 = {\log _{{5^{\frac{1}{2}}}}}2 = 2{\log _5}2 = {\log _5}{2^2} = {\log _5}4\)
Hàm số \(y = {\log _5}x\) có cơ số \(5 > 1\) nên đồng biến trên \(\left( {0; + \infty } \right)\).
Mà \(4 > 2\sqrt 2 \) nên \({\log _5}4 > {\log _5}2\sqrt 2 \). Vậy \({\log _{\sqrt 5 }}2 > {\log _5}2\sqrt 2 \)
c) \( - {\log _{\frac{1}{4}}}2 = - {\log _{{{\left( {\frac{1}{2}} \right)}^2}}}2 = - \frac{1}{2}{\log _{\frac{1}{2}}}2 = {\log _{\frac{1}{2}}}{2^{ - \frac{1}{2}}} = {\log _{\frac{1}{2}}}\frac{1}{{\sqrt 2 }}\)
Hàm số \(y = {\log _{\frac{1}{2}}}x\) có cơ số \(\frac{1}{2} < 1\) nên nghịch biến trên \(\left( {0; + \infty } \right)\).
Mà \(\frac{1}{{\sqrt 2 }} > 0,4\) nên \({\log _{\frac{1}{2}}}\frac{1}{{\sqrt 2 }} < {\log _{\frac{1}{2}}}0,4\). Vậy \( - {\log _{\frac{1}{4}}}2 < {\log _{\frac{1}{2}}}0,4\)
Mức cường độ âm được tính theo công thức như ở Ví dụ 6.
a) Tiếng thì thầm có cường độ âm \(I = {10^{ - 10}}W/{m^2}\) thì có mức cường độ âm bằng bao nhiêu?
b) Để nghe trong thời gian dài mà không gây hại cho tai, âm thanh phải có cường độ không vượt quá 100 000 lần cường độ của tiếng thì thẩm. Âm thanh không gây hại cho tai khi nghe trong thời gian dài phải ở mức cường độ âm như thế nào?
Phương pháp giải:
Sử dụng công thức tính mức cường độ âm \(L = 10\log \left( {\frac{I}{{{I_0}}}} \right)\left( {dB} \right)\) với \({I_0} = {10^{ - 12}}W/{m^2}\).
Lời giải chi tiết:
a) Mức cường độ âm của tiếng thì thầm là:
\(L = 10\log \left( {\frac{I}{{{I_0}}}} \right) = 10\log \left( {\frac{{{{10}^{ - 10}}}}{{{{10}^{ - 12}}}}} \right) = 20\left( {dB} \right)\)
b) Để âm thanh không gây hại cho tai, âm thanh phải có cường độ âm không vượt quá:
\(I = {100000.10^{ - 10}} = 1{0^{ - 5}}W/{m^2}\)
Âm thanh không gây hại cho tai nghe trong thời gian dài phải ở mức cường độ âm không vượt quá:
\(L = 10\log \left( {\frac{I}{{{I_0}}}} \right) = 10\log \left( {\frac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}}} \right) = 70\left( {dB} \right)\)
Mục 2 của chương trình Toán 11 tập 2 - Chân trời sáng tạo thường tập trung vào các kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức hình học nâng cao hơn trong chương trình.
Các bài tập trang 22 thường xoay quanh việc nhận biết và xác định các yếu tố của phép tịnh tiến. Các em cần hiểu rõ định nghĩa, tính chất của phép tịnh tiến và cách biểu diễn phép tịnh tiến bằng phương trình.
Trang 23 tập trung vào phép quay. Các em cần nắm vững định nghĩa, tính chất của phép quay, tâm quay, góc quay và cách xác định ảnh của một điểm, một đường thẳng qua phép quay.
Trang 24 giới thiệu về phép đối xứng trục và phép đối xứng tâm. Các em cần hiểu rõ định nghĩa, tính chất của hai phép biến hình này, trục đối xứng, tâm đối xứng và cách xác định ảnh của một điểm, một đường thẳng qua phép đối xứng.
| Phép biến hình | Định nghĩa | Tính chất |
|---|---|---|
| Phép đối xứng trục | Biến mỗi điểm thành điểm đối xứng của nó qua một trục cho trước. | Bảo toàn khoảng cách giữa hai điểm bất kỳ. |
| Phép đối xứng tâm | Biến mỗi điểm thành điểm đối xứng của nó qua một tâm cho trước. | Bảo toàn khoảng cách giữa hai điểm bất kỳ. |
Để giải các bài tập về phép biến hình, các em cần:
Trong quá trình học tập, các em nên:
Hy vọng với những hướng dẫn chi tiết và dễ hiểu trên đây, các em sẽ tự tin giải quyết các bài tập trong mục 2 trang 22, 23, 24 SGK Toán 11 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!