Chào mừng các em học sinh đến với bài giải bài tập 10.29 trang 132 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Để điều tra sức mua của thị trường, siêu thị U tìm hiểu số tiền ghi trên hoá đơn của một số khách hàng được chọn ngẫu nhiên. Kết quả thống kê được ghi lại trong bảng sau: a) Lập bảng tần số - tần số tương đối ghép nhóm, với các nhóm ghép [100;200), [200;300), [300;400), [400;500), [500;600] (làm tròn kết quả đến hàng phần chục nghìn trước khi chuyển sang viết tần số tương đối ở dạng phần trăm). b) Dựa vào kết quả của câu a, hãy cho biết nhóm khách hàng nào đông nhất và nhóm khách hàng nào í
Đề bài
Để điều tra sức mua của thị trường, siêu thị U tìm hiểu số tiền ghi trên hoá đơn của một số khách hàng được chọn ngẫu nhiên. Kết quả thống kê được ghi lại trong bảng sau:
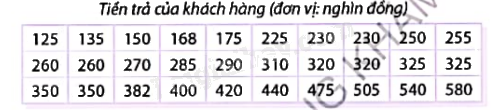
a) Lập bảng tần số - tần số tương đối ghép nhóm, với các nhóm ghép [100;200), [200;300), [300;400), [400;500), [500;600] (làm tròn kết quả đến hàng phần chục nghìn trước khi chuyển sang viết tần số tương đối ở dạng phần trăm).
b) Dựa vào kết quả của câu a, hãy cho biết nhóm khách hàng nào đông nhất và nhóm khách hàng nào ít nhất. Tỉ lệ khách hàng chi tiêu ở mức tối thiểu là 400000 đồng chiếm bao nhiêu phần trăm?
c) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột và dạng đoạn thẳng.
Phương pháp giải - Xem chi tiết
Công thức tính tần tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \).
Bảng tần số - tần số tương đối ghép nhóm là bảng có cả dòng (cột) tần số và dòng (cột) tần số tương đối ghép nhóm.
Dựa vào bảng tần số - tần số tương đối ghép nhóm trả lời câu hỏi.
Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột và dạng đoạn thẳng.
Lời giải chi tiết
a) Bảng tần số - tần số tương đối
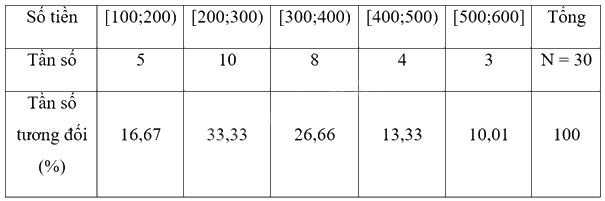
b) Nhóm khách hàng đông nhất là [200;300), nhóm khách hàng ít nhất là [500;600]. Tỉ lệ khách hàng chi tiêu ở mức tối thiểu là 400000 đồng chiếm bao 13,33%.
c) Biểu đồ tương đối ghép nhóm dạng cột:
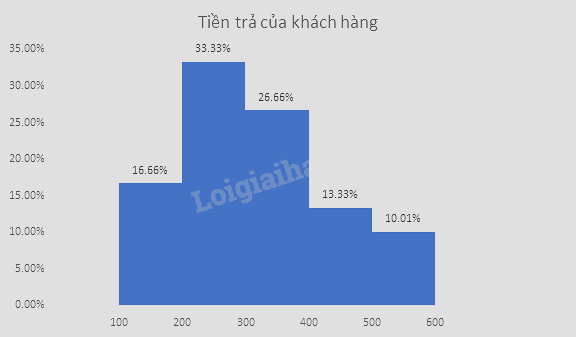
Biểu đồ dạng đoạn thẳng:
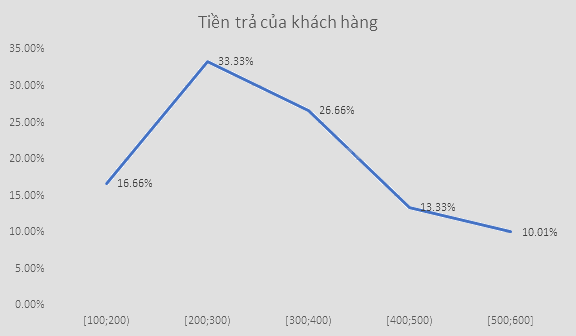
Bài tập 10.29 trang 132 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tìm phương trình tiếp tuyến của một đường cong tại một điểm cho trước, hoặc xác định điều kiện để một đường thẳng là tiếp tuyến của một đường cong.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài tập 10.29, các em cần:
(Ở đây sẽ là lời giải chi tiết cho bài tập 10.29, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết quả cuối cùng. Ví dụ, nếu bài toán yêu cầu tìm phương trình tiếp tuyến của parabol y = x2 tại điểm (1; 1), lời giải sẽ bao gồm các bước sau:)
Vậy phương trình tiếp tuyến của parabol y = x2 tại điểm (1; 1) là y = 2x - 1.
Ngoài bài tập 10.29, còn rất nhiều bài tập tương tự liên quan đến phương pháp tiếp tuyến. Các em có thể tham khảo các bài tập sau:
Để giải các bài tập này, các em cần nắm vững lý thuyết, luyện tập thường xuyên và áp dụng linh hoạt các công thức và phương pháp đã học.
Để củng cố kiến thức và kỹ năng giải bài tập về phương pháp tiếp tuyến, các em có thể tự giải thêm các bài tập sau:
Bài tập 10.29 trang 132 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu sâu hơn về phương pháp tiếp tuyến và ứng dụng của nó. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!