Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 3 trang 65, 66 SGK Toán 9 tập 2. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt trong môn Toán.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải một cách cẩn thận, kèm theo các bước giải thích rõ ràng, giúp các em hiểu sâu sắc bản chất của bài toán.
Trong một thí nghiệm, bạn Mai thả một khối sắt hình trụ có chiều cao h = 6,5 cm, bán kính đáy r = 3,5 cm vào một bình chia độ đang chứa 500 ml nước. Sau khi khối sắt chìm hẳn xuống, bạn Mai thấy mực nước trong bình tăng lên vạch 750ml. Biết 1 ml = 1 cm3.
Trả lời câu hỏi Luyện tập 3 trang 66SGK Toán 9 Cùng khám phá
Tính chiều cao và thể tích của một hình trụ có bán kính đáy bằng 5 cm và diện tích xung quanh bằng \(30\pi \)cm2.
Phương pháp giải:
Diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)
Lời giải chi tiết:
Ta có: \({S_{xq}} = 2\pi rh = 30\pi \)
suy ra h = \(\frac{{30\pi }}{{2\pi .5}} = 3\) cm.
Thể tích hình trụ là:
V = \(\pi {r^2}h = \pi {.5^2}.3 = 75\pi \) (cm3).
Trả lời câu hỏi Vận dụng 2 trang 66SGK Toán 9 Cùng khám phá
Tính thể tích nhựa cần dùng để sản xuất đoạn ống nhựa có kích thức như Hình 9.9.
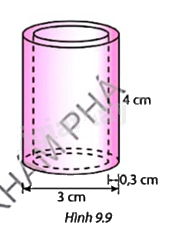
Phương pháp giải:
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)
Lời giải chi tiết:
Thể tích cả đoạn ống nhựa là:
V = \(\pi {r^2}h = \pi .1,{5^2}.4 = 9c{m^3}\)
Thể tích lõi trong ống nhựa là:
Vlõi \( = \pi {r^2}h = \pi .{\left( {\frac{{3 - 2.0,3}}{2}} \right)^2}.4 = 5,76c{m^3}\)
Thể tích nhựa cần dùng là:
Vnhựa = 9 – 5,76 = 3,24 cm3.
Trả lời câu hỏi Hoạt động 3 trang 65 SGK Toán 9 Cùng khám phá
Trong một thí nghiệm, bạn Mai thả một khối sắt hình trụ có chiều cao h = 6,5 cm, bán kính đáy r = 3,5 cm vào một bình chia độ đang chứa 500 ml nước. Sau khi khối sắt chìm hẳn xuống, bạn Mai thấy mực nước trong bình tăng lên vạch 750ml. Biết 1 ml = 1 cm3.

a) Dựa vào mực nước tăng lên trong bình, hãy tính thể tích của khối sắt.
b) Gọi S là diện tích đáy của khối sắt. So sánh tích S.h với kết quả ở câu a và rút ra nhận xét.
Phương pháp giải:
Dựa vào diện tích đường tròn: S = \(\pi {r^2}\) rồi so sánh với câu a.
Lời giải chi tiết:
a) Sự chênh lệch mực nước giữa trước và sau khi cho khối sắt là:
750 – 500 = 250 ml = 250 cm3
Thể tích của khối sắt là 250 cm3.
a) Diện tích đáy của khối sắt là:
S = \(\pi .3,{5^2} = 12,25\) cm2
Suy ra S.h = \(12,25\pi \).6,5 \( \approx 250\) bằng với kết quả câu a
Nhận xét: Thể tích của hình trụ bằng diện tích đáy nhân chiều cao.
Trả lời câu hỏi Hoạt động 3 trang 65 SGK Toán 9 Cùng khám phá
Trong một thí nghiệm, bạn Mai thả một khối sắt hình trụ có chiều cao h = 6,5 cm, bán kính đáy r = 3,5 cm vào một bình chia độ đang chứa 500 ml nước. Sau khi khối sắt chìm hẳn xuống, bạn Mai thấy mực nước trong bình tăng lên vạch 750ml. Biết 1 ml = 1 cm3.

a) Dựa vào mực nước tăng lên trong bình, hãy tính thể tích của khối sắt.
b) Gọi S là diện tích đáy của khối sắt. So sánh tích S.h với kết quả ở câu a và rút ra nhận xét.
Phương pháp giải:
Dựa vào diện tích đường tròn: S = \(\pi {r^2}\) rồi so sánh với câu a.
Lời giải chi tiết:
a) Sự chênh lệch mực nước giữa trước và sau khi cho khối sắt là:
750 – 500 = 250 ml = 250 cm3
Thể tích của khối sắt là 250 cm3.
a) Diện tích đáy của khối sắt là:
S = \(\pi .3,{5^2} = 12,25\) cm2
Suy ra S.h = \(12,25\pi \).6,5 \( \approx 250\) bằng với kết quả câu a
Nhận xét: Thể tích của hình trụ bằng diện tích đáy nhân chiều cao.
Trả lời câu hỏi Luyện tập 3 trang 66SGK Toán 9 Cùng khám phá
Tính chiều cao và thể tích của một hình trụ có bán kính đáy bằng 5 cm và diện tích xung quanh bằng \(30\pi \)cm2.
Phương pháp giải:
Diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)
Lời giải chi tiết:
Ta có: \({S_{xq}} = 2\pi rh = 30\pi \)
suy ra h = \(\frac{{30\pi }}{{2\pi .5}} = 3\) cm.
Thể tích hình trụ là:
V = \(\pi {r^2}h = \pi {.5^2}.3 = 75\pi \) (cm3).
Trả lời câu hỏi Vận dụng 2 trang 66SGK Toán 9 Cùng khám phá
Tính thể tích nhựa cần dùng để sản xuất đoạn ống nhựa có kích thức như Hình 9.9.
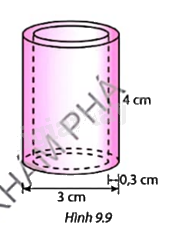
Phương pháp giải:
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)
Lời giải chi tiết:
Thể tích cả đoạn ống nhựa là:
V = \(\pi {r^2}h = \pi .1,{5^2}.4 = 9c{m^3}\)
Thể tích lõi trong ống nhựa là:
Vlõi \( = \pi {r^2}h = \pi .{\left( {\frac{{3 - 2.0,3}}{2}} \right)^2}.4 = 5,76c{m^3}\)
Thể tích nhựa cần dùng là:
Vnhựa = 9 – 5,76 = 3,24 cm3.
Mục 3 trang 65, 66 SGK Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai, và các ứng dụng của chúng. Các bài tập trong mục này yêu cầu học sinh vận dụng kiến thức về định nghĩa, tính chất, đồ thị của hàm số, cũng như các phương pháp giải phương trình, hệ phương trình liên quan.
Bài tập này thường yêu cầu học sinh xác định xem một biểu thức có phải là hàm số hay không, và nếu có thì xác định tập xác định và tập giá trị của hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa về hàm số: một quan hệ giữa hai tập hợp, trong đó mỗi phần tử của tập xác định tương ứng với duy nhất một phần tử của tập giá trị.
Vẽ đồ thị hàm số là một kỹ năng quan trọng trong môn Toán. Để vẽ đồ thị hàm số, học sinh cần xác định các điểm thuộc đồ thị, sau đó nối các điểm này lại với nhau. Trong trường hợp hàm số bậc nhất, đồ thị là một đường thẳng. Trong trường hợp hàm số bậc hai, đồ thị là một parabol.
Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình tương ứng với hai đường thẳng đó. Nghiệm của hệ phương trình chính là tọa độ của giao điểm.
Các bài toán ứng dụng hàm số thường liên quan đến các tình huống thực tế như tính quãng đường, vận tốc, thời gian, hoặc tính lợi nhuận, chi phí. Để giải các bài toán này, học sinh cần xây dựng mô hình toán học phù hợp, sau đó giải phương trình hoặc hệ phương trình để tìm ra kết quả.
Bài tập: Cho hàm số y = 2x + 1. Tìm giá trị của y khi x = 3.
Giải: Thay x = 3 vào hàm số, ta được y = 2 * 3 + 1 = 7. Vậy, khi x = 3 thì y = 7.
Giải mục 3 trang 65, 66 SGK Toán 9 tập 2 đòi hỏi học sinh phải nắm vững kiến thức về hàm số và các phương pháp giải bài tập liên quan. Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết các bài tập trong mục này và đạt kết quả tốt trong môn Toán. Chúc các em học tập tốt!