Chào mừng bạn đến với bài học về Lý thuyết Tiếp tuyến của đường tròn Toán 9 tại giaitoan.edu.vn. Đây là một trong những kiến thức quan trọng giúp bạn hiểu sâu hơn về đường tròn và các tính chất liên quan.
Bài học này sẽ cung cấp cho bạn những khái niệm cơ bản, tính chất quan trọng và các ứng dụng thực tế của tiếp tuyến, giúp bạn tự tin giải các bài toán liên quan.
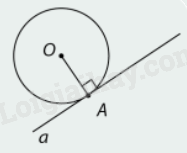
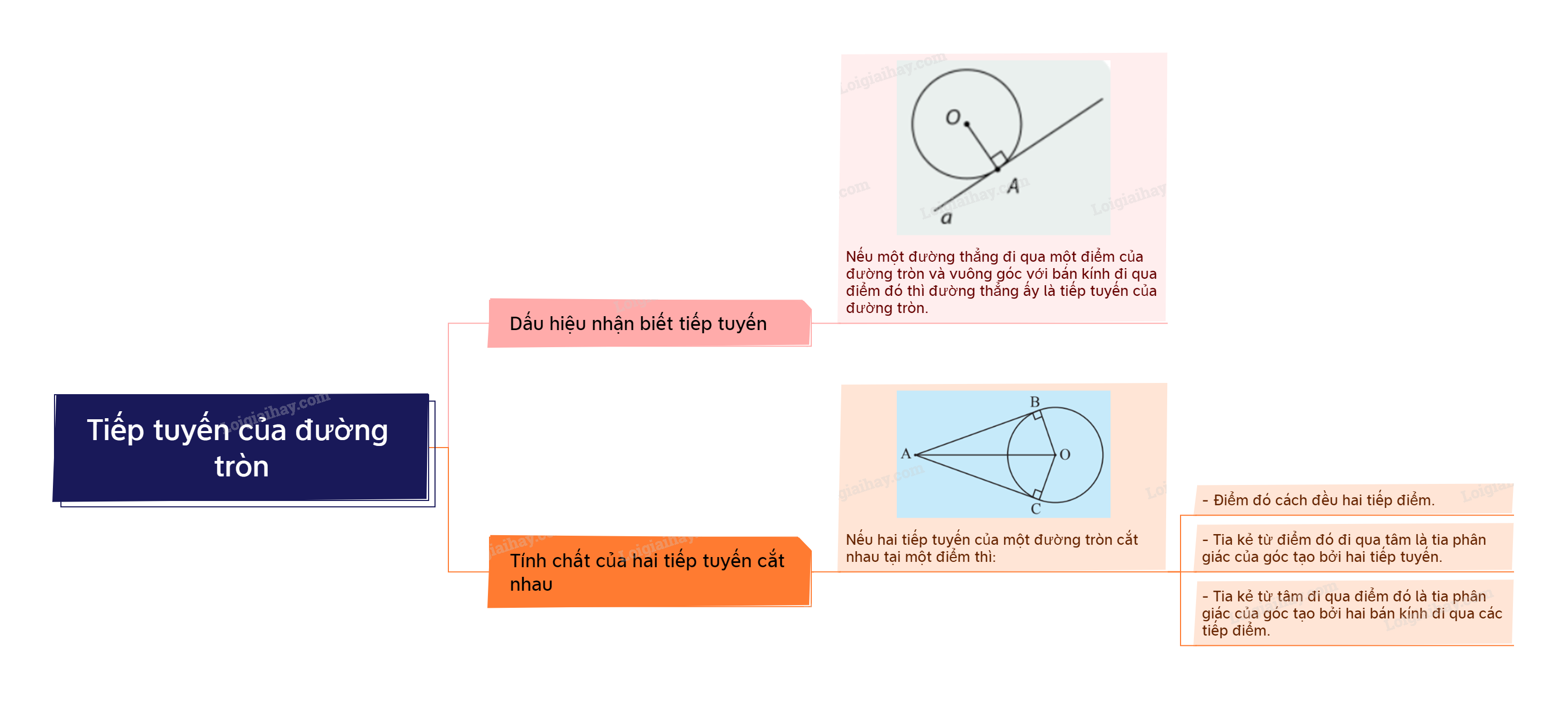
1. Dấu hiệu nhận biết tiếp tuyến của đường tròn Nếu một đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là một tiếp tuyến của đường tròn.
1. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Nếu một đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là một tiếp tuyến của đường tròn. |
2. Tính chất của hai tiếp tuyến cắt nhau
Định lí
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: - Điểm đó cách đều hai tiếp điểm. - Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. - Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm. |
Ví dụ: Cho đường tròn (O), B, C \( \in \) (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.
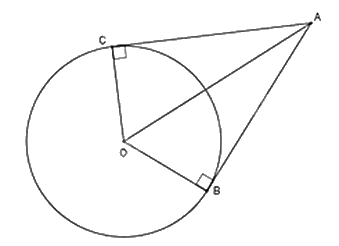
Khi đó:
- AB = AC
- Tia AO là tia phân giác của \(\widehat {BAC}\).
- Tia OA là tia phân giác của \(\widehat {BOC}\).
Tiếp tuyến của đường tròn là một khái niệm quan trọng trong hình học lớp 9. Để nắm vững kiến thức này, chúng ta cần hiểu rõ định nghĩa, tính chất và các ứng dụng của tiếp tuyến.
Tiếp tuyến của một đường tròn là một đường thẳng có đúng một điểm chung với đường tròn. Điểm chung đó được gọi là tiếp điểm.
Ví dụ: Đường thẳng d là tiếp tuyến của đường tròn (O) tại điểm A nếu d chỉ cắt đường tròn (O) tại A.
Một trong những tính chất quan trọng nhất của tiếp tuyến là tiếp tuyến tại một điểm của đường tròn vuông góc với bán kính tại điểm đó.
Định lý: Nếu tiếp tuyến d của đường tròn (O) tại điểm A thì OA ⊥ d.
Chứng minh: (Chứng minh dựa trên kiến thức về khoảng cách từ tâm đường tròn đến đường thẳng)
Từ một điểm nằm ngoài đường tròn, ta có thể kẻ được hai tiếp tuyến đến đường tròn. Hai tiếp tuyến này có tính chất đối xứng qua đường thẳng nối điểm đó với tâm đường tròn.
Định lý: Từ một điểm A nằm ngoài đường tròn (O), kẻ hai tiếp tuyến AB và AC với đường tròn (B và C là tiếp điểm). Khi đó:
Độ dài đoạn thẳng tiếp tuyến có thể được tính toán dựa trên các định lý và công thức liên quan.
Định lý: Nếu từ một điểm A nằm ngoài đường tròn (O), kẻ tiếp tuyến AB đến đường tròn (B là tiếp điểm) và một cát tuyến ACD thì:
AB2 = AC.AD
Bài toán 1: Cho đường tròn (O) đường kính 10cm. Từ một điểm A nằm ngoài đường tròn, kẻ tiếp tuyến AB đến đường tròn (B là tiếp điểm). Biết OA = 12cm. Tính độ dài AB.
Giải:
Bài toán 2: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB và AC đến đường tròn (B và C là tiếp điểm). Gọi M là trung điểm của BC. Chứng minh rằng A, O, M thẳng hàng.
Giải:
Để củng cố kiến thức về Lý thuyết Tiếp tuyến của đường tròn Toán 9, bạn nên thực hành giải nhiều bài tập khác nhau. giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng với các mức độ khó khác nhau, kèm theo đáp án chi tiết để bạn tự kiểm tra và đánh giá kết quả học tập.
Lý thuyết Tiếp tuyến của đường tròn Toán 9 là một phần quan trọng của chương trình học. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức hình học nâng cao hơn. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất!