Chào mừng các em học sinh đến với bài giải bài tập 6.14 trang 18 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
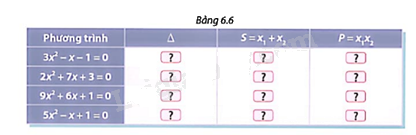
Với mỗi phương trình ở Bảng 6.6: a) Tìm các số thích hợp cho mỗi ô ? ở cột \(\Delta \). b) Nếu phương trình có nghiệm \({x_1};{x_2}\), không giải phương trình, hãy tìm các số thích hợp cho mỗi ô ? ở cột S và P.
Đề bài
Với mỗi phương trình ở Bảng 6.6:
a) Tìm các số thích hợp cho mỗi ô ? ở cột \(\Delta \).
b) Nếu phương trình có nghiệm \({x_1};{x_2}\), không giải phương trình, hãy tìm các số thích hợp cho mỗi ô ? ở cột S và P.
Phương pháp giải - Xem chi tiết
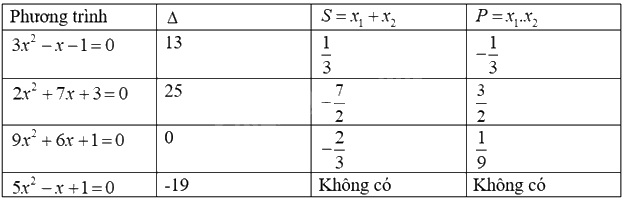
Dựa vào: Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) thì:
\(\left\{ {\begin{array}{*{20}{c}}{S = {x_1} + {x_2} = - \frac{b}{a}}\\{P = {x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Lời giải chi tiết
Bài tập 6.14 trang 18 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = (m-1)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số m-1 khác 0. Bài viết này sẽ đi sâu vào phân tích điều kiện này, cách xác định giá trị của m để hàm số là hàm số bậc nhất, và các ví dụ minh họa cụ thể.
Hàm số y = ax + b được gọi là hàm số bậc nhất khi và chỉ khi a khác 0. Trong trường hợp của bài tập này, a = m-1. Do đó, để y = (m-1)x + 3 là hàm số bậc nhất, chúng ta cần có:
m - 1 ≠ 0
Tức là:
m ≠ 1
Ngược lại, nếu m = 1, thì hàm số trở thành:
y = (1-1)x + 3
y = 0x + 3
y = 3
Trong trường hợp này, hàm số trở thành hàm số hằng, không phải là hàm số bậc nhất.
Ví dụ 1: Với m = 2, hàm số trở thành y = (2-1)x + 3 = x + 3. Đây là hàm số bậc nhất vì hệ số của x là 1, khác 0.
Ví dụ 2: Với m = -1, hàm số trở thành y = (-1-1)x + 3 = -2x + 3. Đây là hàm số bậc nhất vì hệ số của x là -2, khác 0.
Ví dụ 3: Với m = 1, hàm số trở thành y = (1-1)x + 3 = 3. Đây là hàm số hằng, không phải là hàm số bậc nhất.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài tập 6.14 trang 18 SGK Toán 9 tập 2 là một bài tập cơ bản giúp các em hiểu rõ điều kiện để một hàm số là hàm số bậc nhất. Việc nắm vững kiến thức này sẽ là nền tảng quan trọng cho các bài học tiếp theo về hàm số và ứng dụng của chúng. Hy vọng với lời giải chi tiết và các ví dụ minh họa, các em đã hiểu rõ cách giải bài tập này. Chúc các em học tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.