Chào mừng các em học sinh đến với bài giải bài tập 2.28 trang 48 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
\(ABCD\) là hình chữ nhật có chiều dài \(AB = 6cm\) và chiều rộng \(AD = 4cm\). \(P\) là trung điểm cạnh \(AD\). Tìm điểm \(M\) trên cạnh \(CD\) sao cho diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ \(ABCD\) (Hình 2.5).
Đề bài
\(ABCD\) là hình chữ nhật có chiều dài \(AB = 6cm\) và chiều rộng \(AD = 4cm\). \(P\) là trung điểm cạnh \(AD\). Tìm điểm \(M\) trên cạnh \(CD\) sao cho diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ nhật \(ABCD\) (Hình 2.5).
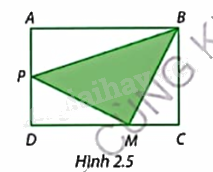
Phương pháp giải - Xem chi tiết
Dựa vào các giải bất phương trình để giải bài toán.
Lời giải chi tiết
Gọi độ dài cạnh \(DM\) là \(x\left( {cm} \right)\).
Diện tích hình chữ nhật \(ABCD\) là: \(AB.AD = 6.4 = 24\left( {c{m^2}} \right)\).
Diện tích tam giác \(APB\) là: \(\frac{1}{2}AP.AB = \frac{1}{2}.2.6 = 6\left( {c{m^2}} \right)\).
Diện tích tam giác \(PDM\) là: \(\frac{1}{2}PD.DM = \frac{1}{2}.2.x = x\left( {c{m^2}} \right)\).
Diện tích tam giác \(BMC\) là: \(\frac{1}{2}.4.\left( {6 - x} \right) = 2\left( {6 - x} \right) = 12 - 2x\left( {c{m^2}} \right)\).
Diện tích tam giác \(PBM\) là: \(24 - 6 - x - \left( {12 - 2x} \right) = 18 - x - 12 + 2x = x + 6\left( {c{m^2}} \right)\).
Để diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ nhật \(ABCD\) thì:
\(\begin{array}{l}x + 6 \le \frac{1}{3}.24\\x + 6 \le 8\\x \le 2\end{array}\)
Vậy điểm \(M\) nằm cách điểm \(D\) nhiều nhất là \(2cm\) thì diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ nhật \(ABCD\).
Bài tập 2.28 trang 48 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về hàm số, bao gồm định nghĩa, tính chất và cách biểu diễn hàm số.
Hàm số bậc nhất có dạng y = ax + b (a ≠ 0). Để xác định hàm số, chúng ta cần biết giá trị của a và b. Các tính chất quan trọng của hàm số bậc nhất bao gồm:
Trước khi đi vào giải bài tập cụ thể, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu chúng ta:
(Giả sử bài tập 2.28 là: Cho hàm số y = 2x - 1. Hãy tìm giá trị của y khi x = 3 và vẽ đồ thị hàm số.)
Bước 1: Tìm giá trị của y khi x = 3
Thay x = 3 vào hàm số y = 2x - 1, ta được:
y = 2 * 3 - 1 = 6 - 1 = 5
Vậy, khi x = 3 thì y = 5.
Bước 2: Vẽ đồ thị hàm sốĐể vẽ đồ thị hàm số y = 2x - 1, chúng ta cần xác định hai điểm thuộc đồ thị. Ta có thể chọn x = 0 và x = 1:
Vẽ đường thẳng đi qua hai điểm A(0, -1) và B(1, 1), ta được đồ thị hàm số y = 2x - 1.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể giải các bài tập tương tự sau:
Khi giải bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Bài tập 2.28 trang 48 SGK Toán 9 tập 1 là một bài tập cơ bản về hàm số bậc nhất. Bằng cách nắm vững lý thuyết và áp dụng các phương pháp giải phù hợp, các em có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!