Chào mừng các em học sinh đến với bài giải bài tập 7.7 trang 34 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
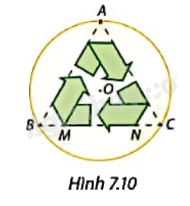
Biểu tượng tái chế trên thiết kế của huy hiệu hình tròn tam O được bạn Minh dựngDựa trên tam giác đều ABC nội tiếp trong (O) như Hình 7.10. Độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC. Tính MN nếu đường kính huy hiệu là 4 cm. Làm tròn kết quả đến hàng phần mười centimet.
Đề bài
Biểu tượng tái chế trên thiết kế của huy hiệu hình tròn tam O được bạn Minh dựng dựa trên tam giác đều ABC nội tiếp trong (O) như Hình 7.10. Độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC. Tính MN nếu đường kính huy hiệu là 4 cm. Làm tròn kết quả đến hàng phần mười centimet.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất tam giác đều để tìm bán kính đường tròn
Áp dụng định lý Pytago để tìm cạnh của tam giác đều
Áp dụng công thức tính diện tích tam giác \(S = \frac{{ah}}{2}\) với ℎ là chiều cao ứng với cạnh đáy là a
Lời giải chi tiết
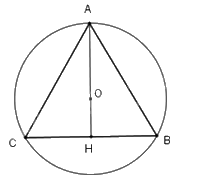
Ta có tam giác ABC đều cạnh a nội tiếp đường tròn (O;R)
Khi đó O là trọng tâm tam giác ABC. Gọi AH là đường trung tuyến.
Suy ra R = AO = \(\frac{2}{3}\)AH suy ra AH = \(\frac{{3R}}{2}\)
Theo định lí Pythagore ta có:
AH2 = AB2 – BH2 = \(\frac{{3{a^2}}}{4}\)suy ra AH = \(\frac{{a\sqrt 3 }}{2}\)
Từ đó ta có \(\frac{{3R}}{2}\) = \(\frac{{a\sqrt 3 }}{2}\) suy ra a = \(\sqrt 3 \)R.
Thay R = \(\frac{4}{2}\)= 2 cm ta được cạnh của tam giác đều BC là: 2\(\sqrt 3 \)cm
Suy ra độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC nên
MN = \(\frac{3}{5}\).2\(\sqrt 3 \) = \(\frac{{6\sqrt 3 }}{5} \approx 2,08cm\)
Bài tập 7.7 trang 34 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = (m-1)x + 2. Bài toán này tập trung vào việc xác định điều kiện của m để hàm số là hàm số bậc nhất, hàm số đồng biến, nghịch biến và vẽ đồ thị hàm số.
Để hàm số y = (m-1)x + 2 là hàm số bậc nhất, hệ số của x phải khác 0. Điều này có nghĩa là:
m - 1 ≠ 0
Suy ra: m ≠ 1
Hàm số y = (m-1)x + 2 đồng biến khi hệ số của x lớn hơn 0:
m - 1 > 0
Suy ra: m > 1
Hàm số y = (m-1)x + 2 nghịch biến khi hệ số của x nhỏ hơn 0:
m - 1 < 0
Suy ra: m < 1
Khi m = 2, hàm số trở thành y = (2-1)x + 2 = x + 2.
Để vẽ đồ thị hàm số y = x + 2, ta cần xác định hai điểm thuộc đồ thị. Ví dụ:
Nối hai điểm A và B, ta được đồ thị hàm số y = x + 2 là một đường thẳng.
Ví dụ 1: Cho hàm số y = (k+1)x - 3. Tìm giá trị của k để hàm số nghịch biến?
Để hàm số nghịch biến, ta cần k + 1 < 0, suy ra k < -1.
Bài tập 1: Cho hàm số y = (2-a)x + 1. Tìm giá trị của a để hàm số là hàm số bậc nhất và đồng biến?
Để hàm số bậc nhất và đồng biến, ta cần 2 - a > 0, suy ra a < 2.
Việc hiểu rõ điều kiện để hàm số là hàm số bậc nhất, đồng biến, nghịch biến là nền tảng quan trọng để giải các bài toán liên quan đến hàm số bậc nhất và ứng dụng trong thực tế. Các em có thể áp dụng kiến thức này để giải quyết các bài toán về đường thẳng, hệ phương trình bậc nhất hai ẩn và các bài toán thực tế liên quan đến sự thay đổi tuyến tính.
Để củng cố kiến thức, các em nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu bản chất của bài toán và áp dụng các công thức, định lý một cách linh hoạt.
Bài tập 7.7 trang 34 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúc các em học tập tốt!