Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 27 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
Dùng phần mềm Geogebra vẽ đồ thị của các hàm số sau và tìm toạ độ giao điểm (nếu có) của hai đồ thị: 1. \(y = \frac{1}{3}{{\rm{x}}^2}\) và \(y = - x + \frac{1}{2}\) 2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \) 3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\)
Đề bài
Trả lời câu hỏi Thực hành trang 27SGK Toán 9 Cùng khám phá
Dùng phần mềm Geogebra vẽ đồ thị của các hàm số sau và tìm toạ độ giao điểm (nếu có) của hai đồ thị:
1. \(y = \frac{1}{3}{{\rm{x}}^2}\) và \(y = - x + \frac{1}{2}\)
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \)
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\)
Phương pháp giải - Xem chi tiết
Bước 1. Vẽ đồ thị hàm số \(y = a{x^2}\).
Nhập lệnh y = ax^2.
Bước 2. Vẽ đồ thị hàm số y = ax + b.
Nhập lệnh y = ax + b.
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng 
để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
Lời giải chi tiết
1. \(y = \frac{1}{3}{x^2}\) và \(y = - x + \frac{1}{2}\).
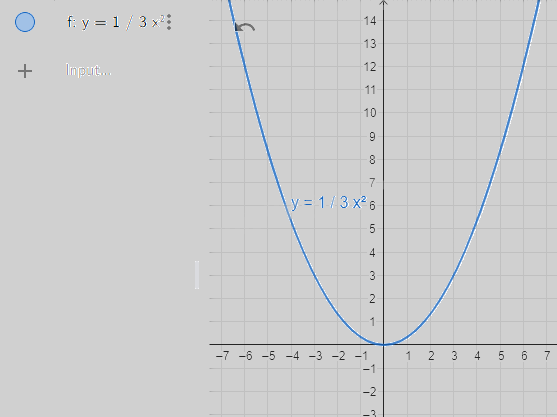
Bước 1. Vẽ đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Nhập lệnh y = 1/3*x^2
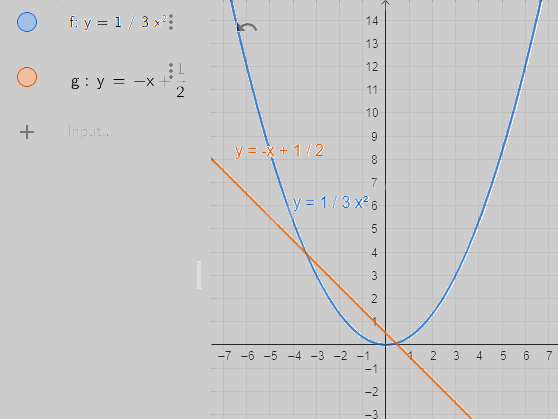
Bước 2. Vẽ đồ thị hàm số \(y = - x + \frac{1}{2}\).
Nhập lệnh y = -x + 1/2
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng 
để tìm giao điểm của hai đồ thị.
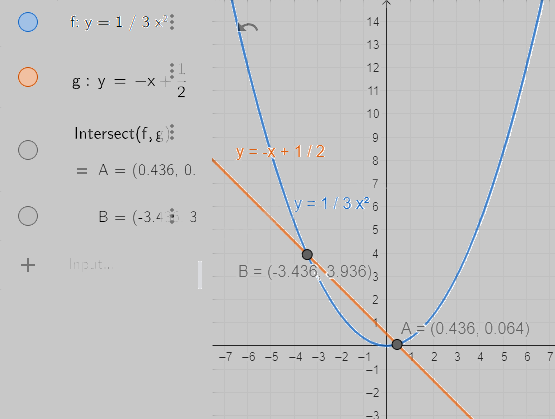
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l}\frac{1}{3}{x^2} = - x + \frac{1}{2}\\\frac{1}{3}{x^2} + x - \frac{1}{2} = 0\end{array}\)
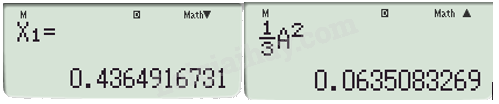
Ta được tọa độ điểm A.
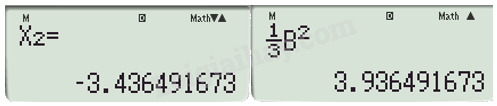
Ta được tọa độ điểm B.
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \).
Bước 1. Vẽ đồ thị hàm số \(y = \sqrt 2 {x^2}\).
Sử dụng bàn phím của GeoGebra để nhập kí hiệu \(\sqrt {...} \)
Ta được màn hình như sau:
Nhập lệnh: \(y = \sqrt 2 *x\^2\)
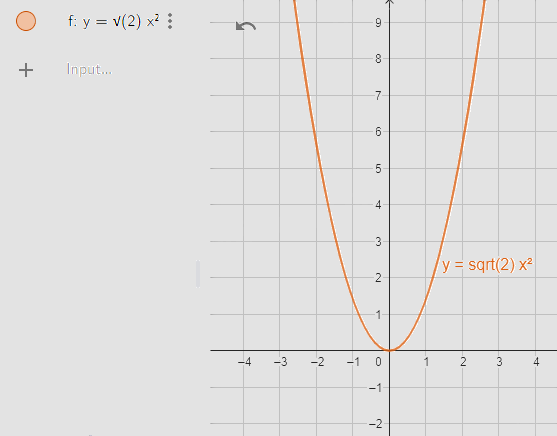
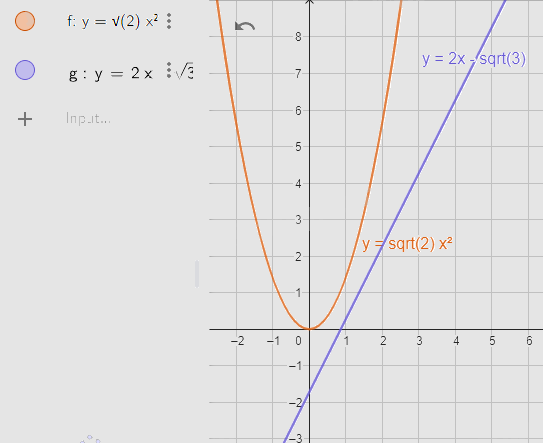
Bước 2. Vẽ đồ thị hàm số \(y = 2x - \sqrt 3 \).
Nhập lệnh \(y = 2x - \sqrt 3 \)
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng 
ta thấy hai đồ thị không có điểm chung.
Do đó không có giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l}\sqrt 2 {x^2} = 2x - \sqrt 3 \\\sqrt 2 {x^2} - 2x + \sqrt 3 = 0\end{array}\)
Sử dụng máy tính cầm tay để giải phương trình, ta được:
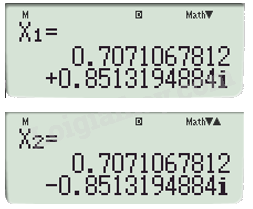
Vậy hai đồ thị không có giao điểm.
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\).
Bước 1. Vẽ đồ thị hàm số \(y = - 1,2{x^2}\).
Nhập lệnh y = -1.2*x^2
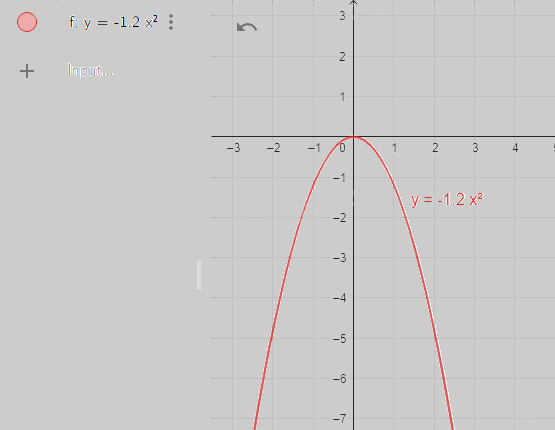
Bước 2. Vẽ đồ thị hàm số \(y = 0,6x + 0,075\).
Nhập lệnh \(y = 0.6x + 0.075\)
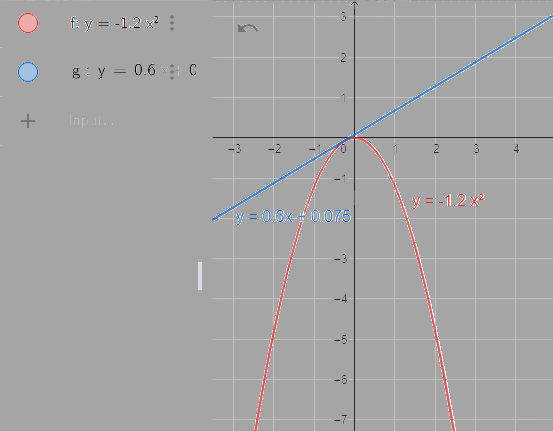
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng 
để tìm giao điểm của hai đồ thị.
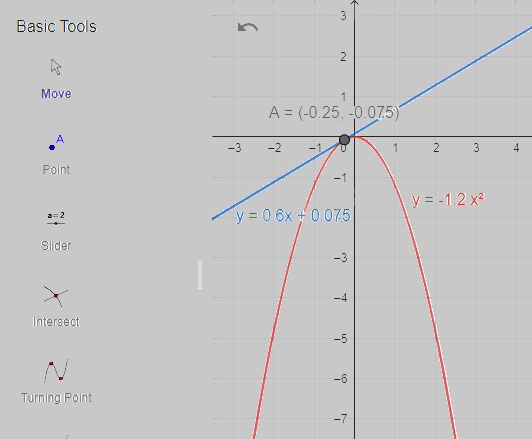
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l} - 1,2{x^2} = 0,6x + 0,075\\ - 1,2{x^2} - 0,6x - 0,075 = 0\end{array}\)
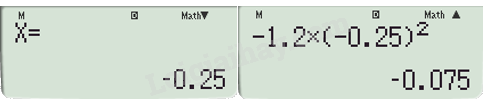
Ta được tọa độ điểm A.
Mục 1 trang 27 SGK Toán 9 tập 2 tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh xác định hệ số góc, phương trình đường thẳng, và ứng dụng các kiến thức về hàm số để giải quyết các bài toán thực tế.
Dưới đây là một số bài tập minh họa và lời giải chi tiết để giúp các em hiểu rõ hơn về nội dung của Mục 1 trang 27 SGK Toán 9 tập 2:
Lời giải: Hệ số góc của đường thẳng y = 2x - 3 là 2.
Lời giải: Để vẽ đồ thị hàm số y = -x + 1, ta xác định hai điểm thuộc đồ thị, ví dụ: A(0; 1) và B(1; 0). Nối hai điểm này lại, ta được đồ thị hàm số.
Lời giải: Để tìm giao điểm của hai đường thẳng y = x + 2 và y = -x + 4, ta giải hệ phương trình:
Thay (1) vào (2), ta được: x + 2 = -x + 4 => 2x = 2 => x = 1. Thay x = 1 vào (1), ta được: y = 1 + 2 = 3. Vậy giao điểm của hai đường thẳng là (1; 3).
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, các em cần nắm vững các kiến thức cơ bản về hàm số, đồ thị hàm số, và ứng dụng của hàm số. Ngoài ra, các em cũng cần luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
Các bài tập về hàm số bậc nhất thường gặp các dạng sau:
Ngoài SGK Toán 9 tập 2, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập bài cũ, làm bài tập đầy đủ, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt!
Giaitoan.edu.vn hy vọng bài giải này sẽ giúp các em hiểu rõ hơn về Mục 1 trang 27 SGK Toán 9 tập 2 và tự tin hơn trong quá trình học tập.
