Chào mừng các em học sinh đến với bài giải bài tập 5.37 trang 127 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Trong Hình 5.74, độ dài cạnh của các hình vuông lớn là 10cm. Tính diện tích và chu vi của phần được tô màu.
Đề bài
Trong Hình 5.74, độ dài cạnh của các hình vuông lớn là 10cm. Tính diện tích và chu vi của phần được tô màu.
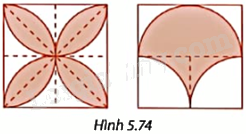
Phương pháp giải - Xem chi tiết
* Hình vẽ gồm 4 cánh hoa tô màu thì:
- Diện tích:
+ Diện tích bốn hình vuông nhỏ bằng nhau, 2 phần không được tô màu ở mỗi hình vuông nhỏ đều bằng nhau và diện tích mỗi cánh hoa đều bằng nhau.
+ Diện tích một cánh hoa trong hình vuông AHOT bằng hiệu diện tích giữa hình vuông AHOT và phần diện tích không được tô màu trong hình vuông AHOT.
+ Diện tích phần không tô màu là: 2. (diện tích hình vuông - \(\frac{1}{4}\) diện tích hình tròn bán kính 5cm).
- Tính chu vi hình bông hoa:
+ Hai cánh nằm trong hình chữ nhật AHSD gồm 4 cung, mỗi cung là một phần tư đường tròn bán kính 5cm.
+ Hai cánh nằm trong hình chữ nhật HSCB gồm 4 cung, mỗi cung là một phần tư đường tròn bán kính 5cm.
Do đó, chu vi của hình tô màu bằng 2 lần chu vi đường tròn bán kính 5cm
* Hình thứ hai:
- Chu vi: Hình gồm hai cung: Một cung là một nửa đường tròn có bán kính 5cm, hai cung mỗi cung là một phần tư đường tròn bán kính 5cm nên chu vi hình bằng chu vi đường tròn bán kính 5cm.
- Diện tích hình bằng tổng:
+ Diện tích nửa hình tròn bán kính 5cm.
+ Diện tích phần tô màu trong hình vuông ABEF và hình vuông BCDE.
(Diện tích tô màu trong mỗi hình vuông bằng hiệu diện tích hình vuông ABEF và \(\frac{1}{4}\) diện tích hình tròn bán kính 5cm)
Lời giải chi tiết
Đặt tên các điểm như hình vẽ.
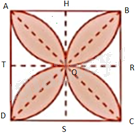
Độ dài mỗi cạnh của hình vuông nhỏ là: \(10:2 = 5cm\).
Ta thấy, diện tích bốn hình vuông nhỏ bằng nhau, 2 phần không được tô màu ở mỗi hình vuông nhỏ đều bằng nhau và diện tích mỗi cánh hoa đều bằng nhau.
Diện tích hình vuông AHOT là:
\({5^2} = 25\left( {c{m^2}} \right)\).
\(\frac{1}{4}\) diện tích hình tròn tâm T, bán kính 5cm là:
\(\frac{1}{4}{.5^2}.\pi = \frac{{25\pi }}{4}\left( {c{m^2}} \right)\).
Diện tích phần không được tô màu trong hình vuông AHOT là:
\(2.\left( {25 - \frac{{25\pi }}{4}} \right)\left( {c{m^2}} \right)\).
Diện tích cánh hoa nằm trong hình vuông AHOT là:
\(25 - 2\left( {25 - \frac{{25\pi }}{4}} \right) = - 25 + \frac{{25\pi }}{2}\left( {c{m^2}} \right)\).
Do đó, diện tích hình cần tính là: \(4.\left( { - 25 + \frac{{25\pi }}{2}} \right) = - 100 + 50\pi \left( {c{m^2}} \right)\).
Hình trên gồm bốn cánh hoa, trong đó:
+ Hai cánh nằm trong hình chữ nhật AHSD gồm 4 cung, mỗi cung là một phần tư đường tròn bán kính 5cm.
+ Hai cánh nằm trong hình chữ nhật HSCB gồm 4 cung, mỗi cung là một phần tư đường tròn bán kính 5cm.
Do đó, chu vi của hình tô màu bằng 2 lần chu vi đường tròn bán kính 5cm, tức là: \(2.2.5\pi = 20\pi \left( {cm} \right)\)
Hình vẽ thứ hai:
Hình gồm hai cung: Một cung là một nửa đường tròn có bán kính 5cm, hai cung mỗi cung là một phần tư đường tròn bán kính 5cm nên chu vi hình bằng chu vi đường tròn bán kính 5cm.
Vậy chu vi hình vẽ là: \(2\pi .5 = 10\pi \left( {cm} \right)\)
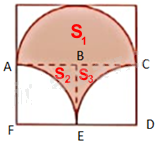
Đặt tên các điểm như hình vẽ.
Diện tích nửa hình tròn bán kính 5cm là:
\({S_1} = {5^2}\pi = 25\pi \left( {c{m^2}} \right)\).
Diện tích hình vuông BCDE là:
\({S_{BCDE}} = {5^2} = 25\left( {c{m^2}} \right)\)
Phần không tô màu trong hình vuông BCDE là một phần tư hình tròn bán kính 5cm nên diện tích phần không tô màu trong hình vuông BCDE là:
\(S = \frac{1}{4}{.5^2}\pi = \frac{{25\pi }}{4}\left( {c{m^2}} \right)\).
Diện tích phần tô màu trong hình vuông BCDE là:
\({S_2} = {S_{BCDE}} - S = 25\pi - \frac{{25}}{4}\pi = \frac{{75\pi }}{4}\left( {c{m^2}} \right)\).
Tương tự ta có, diện tích phần tô màu trong hình vuông ABEF là:
\({S_3} = \frac{{75\pi }}{4}\left( {c{m^2}} \right)\).
Vậy diện tích phần tô màu là:
\({S_1} + {S_2} + {S_3} = 25\pi + \frac{{75\pi }}{4} + \frac{{75\pi }}{4} = \frac{{125\pi }}{2}\left( {c{m^2}} \right)\).
Bài tập 5.37 trang 127 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất và ứng dụng. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.
Thông thường, đề bài sẽ yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết của bài tập 5.37, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Bài 5.37: Cho hàm số y = 2x + 3. Hãy tìm các giá trị của x sao cho y > 0.
Lời giải:
Để y > 0, ta có:
2x + 3 > 0
2x > -3
x > -3/2
Vậy, các giá trị của x thỏa mãn y > 0 là x > -3/2.
Ngoài bài tập 5.37, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để nắm vững kiến thức về hàm số bậc nhất và ứng dụng, các em nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, các em có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn cùng lớp.
Bài tập 5.37 trang 127 SGK Toán 9 tập 1 là một bài tập điển hình về hàm số bậc nhất. Việc nắm vững kiến thức cơ bản và phương pháp giải sẽ giúp các em giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số góc | a, thể hiện độ dốc của đường thẳng |
| Tung độ gốc | b, là giá trị của y khi x = 0 |