Chào mừng bạn đến với bài học về lý thuyết căn bậc ba và căn thức bậc ba trong chương trình Toán 9 tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng, các định nghĩa, tính chất quan trọng và phương pháp giải các bài toán liên quan.
Chúng tôi tin rằng, với sự hướng dẫn chi tiết và bài tập thực hành phong phú, bạn sẽ dễ dàng nắm vững kiến thức và tự tin áp dụng vào giải quyết các bài toán thực tế.
1. Khái niệm về căn bậc ba của một số thực Căn bậc ba của một số thực a là số x sao cho \({x^3} = a\). Chú ý: - Mỗi số a đều có duy nhất một căn bậc ba. - Căn bậc ba của số thực a được kí hiệu là \(\sqrt[3]{a}\), trong đó số 3 được gọi là chỉ số của căn.
1. Khái niệm về căn bậc ba của một số thực
Căn bậc ba của một số thực a là số x sao cho \({x^3} = a\). |
Chú ý:
- Mỗi số a đều có duy nhất một căn bậc ba.
- Căn bậc ba của số thực a được kí hiệu là \(\sqrt[3]{a}\), trong đó số 3 được gọi là chỉ số của căn.
Từ định nghĩa căn bậc ba, ta có \({\left( {\sqrt[3]{a}} \right)^3} = \sqrt[3]{{{a^3}}} = a\) với mọi số thực a.
- Phép tìm căn bậc ba của một số thực gọi là phép khai căn bậc ba.
Ví dụ:
\(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\);
\(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\).
Nhận xét: Căn bậc ba của số dương là số dương, căn bậc ba của số âm là số âm, căn bậc ba của số 0 là số 0.
Tính chất của căn bậc ba:
Với hai số thực a và b:
- Nếu \(a < b\) thì \(\sqrt[3]{a} < \sqrt[3]{b}\);
\(\sqrt[3]{{ab}} = \sqrt[3]{a}.\sqrt[3]{b}\);
\(\sqrt[3]{{\frac{a}{b}}} = \frac{{\sqrt[3]{a}}}{{\sqrt[3]{b}}}\) nếu \(b \ne 0\).
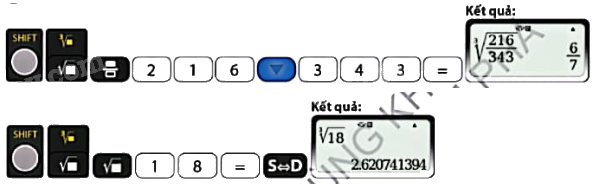
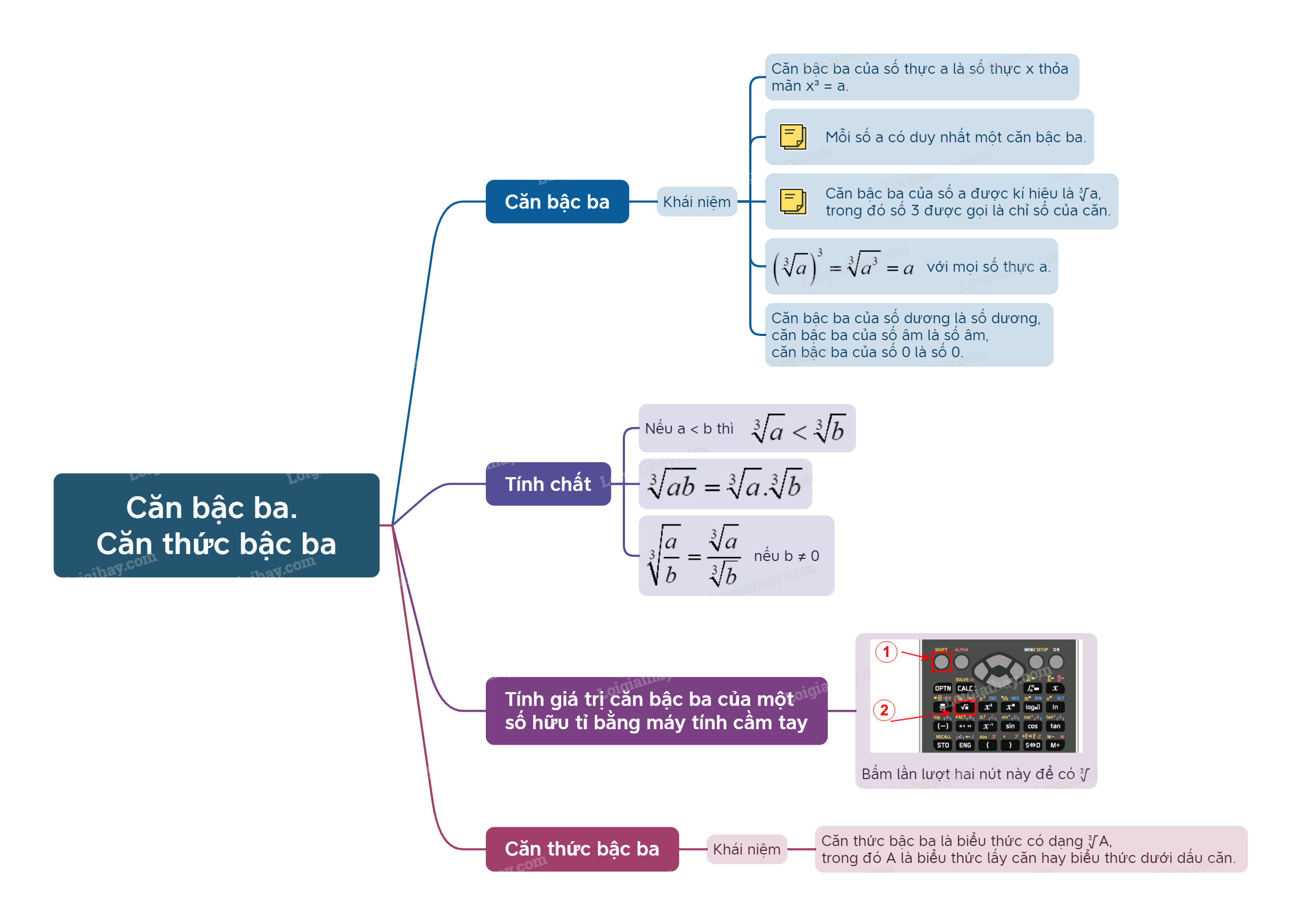
2. Tính giá trị căn bậc ba của một số hữu tỉ bằng máy tính cầm tay
Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

Ví dụ:
2. Căn thức bậc ba của một biểu thức đại số
Khái niệm
Với A là một biểu thức đại số, người ta gọi \(\sqrt[3]{A}\) là căn thức bậc ba của A, còn A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn. |
Ví dụ:
\(\sqrt[3]{{{a^9}}} = {a^3}\); \(\frac{{\sqrt[3]{{2{y^3}}}}}{{\sqrt[3]{{128}}}} = \sqrt[3]{{\frac{{2{y^3}}}{{128}}}} = \sqrt[3]{{\frac{{{y^3}}}{{64}}}} = \frac{{\sqrt[3]{{{y^3}}}}}{{\sqrt[3]{{64}}}} = \frac{y}{4}\).
Trong chương trình Toán 9, căn bậc ba và căn thức bậc ba là một phần quan trọng của chương trình đại số. Hiểu rõ lý thuyết và cách áp dụng chúng là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong tương lai. Bài viết này sẽ cung cấp một cái nhìn toàn diện về chủ đề này, bao gồm định nghĩa, tính chất, các phép toán và ứng dụng thực tế.
Căn bậc ba của một số thực a, ký hiệu là ∛a, là số thực x sao cho x3 = a. Nói cách khác, x là số mà khi nhân với chính nó ba lần sẽ cho ra a.
Căn thức bậc ba là biểu thức có dạng ∛A, trong đó A là một biểu thức đại số. Căn thức bậc ba cũng tuân theo các quy tắc tương tự như căn bậc hai, nhưng với bậc là 3.
Một số tính chất quan trọng của căn bậc ba bao gồm:
Chỉ có thể cộng hoặc trừ các căn bậc ba đồng dạng, tức là các căn thức có cùng biểu thức bên trong căn.
Ví dụ: 2∛5 + 3∛5 = 5∛5
Để nhân hoặc chia các căn bậc ba, ta áp dụng các tính chất đã nêu ở trên.
Ví dụ:
Để khử mẫu của một căn thức bậc ba, ta nhân cả tử và mẫu của phân số chứa căn thức với một biểu thức thích hợp để mẫu trở thành một số lập phương hoàn chỉnh.
Ví dụ: Để khử mẫu của ∛(2/3), ta nhân cả tử và mẫu với ∛(32) = ∛9:
∛(2/3) = (∛2 * ∛9) / (∛3 * ∛9) = ∛18 / ∛27 = ∛18 / 3
Dưới đây là một số bài tập để bạn luyện tập:
Căn bậc ba và căn thức bậc ba được ứng dụng trong nhiều lĩnh vực khác nhau, bao gồm:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết căn bậc ba và căn thức bậc ba Toán 9. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan. Chúc bạn học tốt!