Bạn đang gặp khó khăn trong việc giải các bài tập Toán 9 tập 1 trang 95 và 96? Đừng lo lắng, giaitoan.edu.vn sẽ đồng hành cùng bạn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những giải pháp học tập hiệu quả nhất.
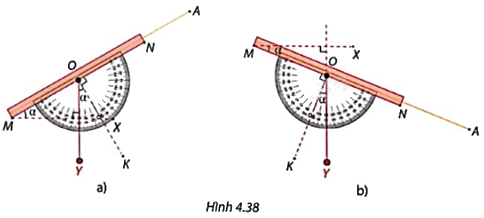
Khi sử dụng giác kế đứng, người ta đặt mắt ở vị trí M và hướng ống ngắm MN về phía điểm A cần quan sát như trong Hình 4.38. Góc AMX giữa hướng nhìn và phương ngang được gọi là góc nâng của A (so với M) nếu hướng nhìn xiên lên trên (Hình 4.38a) hoặc gọi là góc hạ của A (so với M) nếu hướng nhìn xiên xuống dưới (Hình 4.38b). Vì sao góc AMX luôn bằng góc KOY tạo bởi dây dọi và tia OK đi qua vạch \({90^o}\)?
Trả lời câu hỏi Hoạt động 2 trang 96 SGK Toán 9 Cùng khám phá
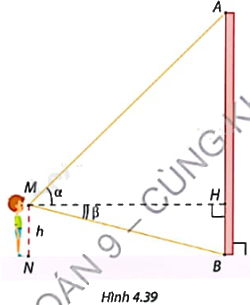
Học sinh thực hiện và trình bày tại lớp lời giải cho bài toán sau: Trong Hình 4.39, chiều cao từ mắt đến mặt đất của bạn học sinh là \(MN = h\left( m \right)\), góc nâng của đỉnh cột A là \(\alpha \) và góc hạ của chân cột B là \(\beta \). Giải thích vì sao \(AB = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\).
Phương pháp giải:
+ Chứng minh tứ giác HBNM là hình chữ nhật, do đó \(HB = MN = h\).
+ Tam giác HBM vuông tại H nên \(HB = MH.\tan \beta \), suy ra \(MH = \frac{{HB}}{{\tan \beta }}\).
+ Tam giác MHA vuông tại H nên \(HA = MH.\tan \alpha = \frac{{HB}}{{\tan \beta }}.\tan \alpha \).
+ Kết hợp với \(AB = HA + HB\), từ đó suy ra điều phải chứng minh.
Lời giải chi tiết:
Tứ giác HBNM có: \(\widehat {MHB} = \widehat {HBN} = \widehat {MNB} = {90^o}\) nên tứ giác HBNM là hình chữ nhật, do đó \(HB = MN = h\).
Tam giác HBM vuông tại H nên \(HB = MH.\tan \beta \), suy ra \(MH = \frac{{HB}}{{\tan \beta }} = \frac{h}{{\tan \beta }}\).
Tam giác MHA vuông tại H nên
\(HA = MH.\tan \alpha = \frac{h}{{\tan \beta }}.\tan \alpha \).
Ta có:
\(AB = HA + HB = \frac{h}{{\tan \beta }}.\tan \alpha + h = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\) (đpcm).
Trả lời câu hỏi Hoạt động 3 trang 96 SGK Toán 9 Cùng khám phá
Đo chiều cao cột cờ
Học sinh thực hiện ngoài trời và trình bày kết quả trước cả lớp.
Sử dụng giác kế và thước để đo góc nâng \(\alpha \) của đỉnh cột cờ, góc hạ \(\beta \) của chân cột cờ và chiều cao h tính từ mắt bạn quan sát đến mặt đất.
Điền các kết quả đo được vào Bảng 4.4 và tính chiều cao cột AB bằng công thức có được từ hoạt động 2.
Thực hiện nhiều lần với các bạn khác nhau và vị trí quan sát khác nhau. So sánh các kết quả tính và nhận xét.

Phương pháp giải:
+ Thực hiện đo góc nâng \(\alpha \) của đỉnh cột cờ, góc hạ \(\beta \) của chân cột cờ và chiều cao h tính từ mắt bạn quan sát đến mặt đất.5/8/2024
+ Áp dụng công thức \(AB = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\) để tính chiều cao cột cờ rồi điền vào bảng.
Lời giải chi tiết:

Các kết quả đo ở các lần là xấp xỉ nhau.
Trả lời câu hỏi Hoạt động 1 trang 95 SGK Toán 9 Cùng khám phá
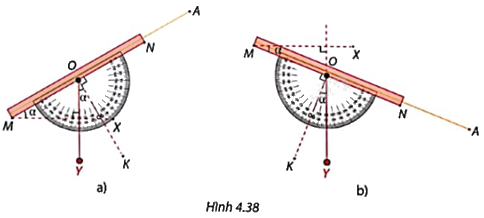
Khi sử dụng giác kế đứng, người ta đặt mắt ở vị trí M và hướng ống ngắm MN về phía điểm A cần quan sát như trong Hình 4.38. Góc AMX giữa hướng nhìn và phương ngang được gọi là góc nâng của A (so với M) nếu hướng nhìn xiên lên trên (Hình 4.38a) hoặc gọi là góc hạ của A (so với M) nếu hướng nhìn xiên xuống dưới (Hình 4.38b). Vì sao góc AMX luôn bằng góc KOY tạo bởi dây dọi và tia OK đi qua vạch \({90^o}\)?
Phương pháp giải:
Sử dụng tính chất của hai góc bù nhau để giải thích.
Lời giải chi tiết:
Trong Hình 4.38a:
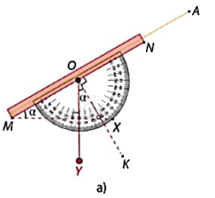
Ta có: \(\widehat {AMX} + \widehat {MOY} = \widehat {KOY} + \widehat {MOY}\left( { = {{90}^o}} \right)\) nên \(\widehat {AMX} = \widehat {KOY}\).
Trong Hình 4.38b: Gọi E là giao điểm của MX và đường thẳng OY.
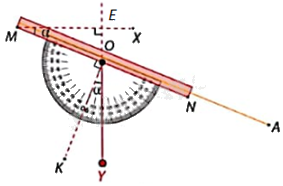
Ta có: \(\widehat {AMX} + \widehat {MOE} = {90^o}\), \(\widehat {KOY} + \widehat {YON} = {90^o}\), \(\widehat {MOE} = \widehat {YON}\) (hai góc đối đỉnh).
Do đó, \(\widehat {AMX} = \widehat {KOY}\).
Trả lời câu hỏi Hoạt động 1 trang 95 SGK Toán 9 Cùng khám phá
Khi sử dụng giác kế đứng, người ta đặt mắt ở vị trí M và hướng ống ngắm MN về phía điểm A cần quan sát như trong Hình 4.38. Góc AMX giữa hướng nhìn và phương ngang được gọi là góc nâng của A (so với M) nếu hướng nhìn xiên lên trên (Hình 4.38a) hoặc gọi là góc hạ của A (so với M) nếu hướng nhìn xiên xuống dưới (Hình 4.38b). Vì sao góc AMX luôn bằng góc KOY tạo bởi dây dọi và tia OK đi qua vạch \({90^o}\)?
Phương pháp giải:
Sử dụng tính chất của hai góc bù nhau để giải thích.
Lời giải chi tiết:
Trong Hình 4.38a:
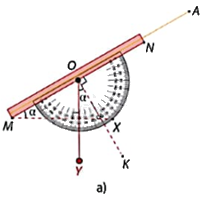
Ta có: \(\widehat {AMX} + \widehat {MOY} = \widehat {KOY} + \widehat {MOY}\left( { = {{90}^o}} \right)\) nên \(\widehat {AMX} = \widehat {KOY}\).
Trong Hình 4.38b: Gọi E là giao điểm của MX và đường thẳng OY.
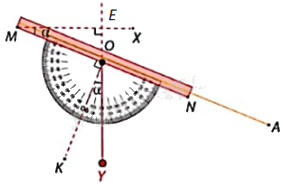
Ta có: \(\widehat {AMX} + \widehat {MOE} = {90^o}\), \(\widehat {KOY} + \widehat {YON} = {90^o}\), \(\widehat {MOE} = \widehat {YON}\) (hai góc đối đỉnh).
Do đó, \(\widehat {AMX} = \widehat {KOY}\).
Trả lời câu hỏi Hoạt động 2 trang 96 SGK Toán 9 Cùng khám phá
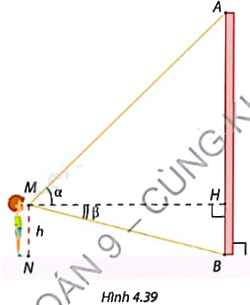
Học sinh thực hiện và trình bày tại lớp lời giải cho bài toán sau: Trong Hình 4.39, chiều cao từ mắt đến mặt đất của bạn học sinh là \(MN = h\left( m \right)\), góc nâng của đỉnh cột A là \(\alpha \) và góc hạ của chân cột B là \(\beta \). Giải thích vì sao \(AB = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\).
Phương pháp giải:
+ Chứng minh tứ giác HBNM là hình chữ nhật, do đó \(HB = MN = h\).
+ Tam giác HBM vuông tại H nên \(HB = MH.\tan \beta \), suy ra \(MH = \frac{{HB}}{{\tan \beta }}\).
+ Tam giác MHA vuông tại H nên \(HA = MH.\tan \alpha = \frac{{HB}}{{\tan \beta }}.\tan \alpha \).
+ Kết hợp với \(AB = HA + HB\), từ đó suy ra điều phải chứng minh.
Lời giải chi tiết:
Tứ giác HBNM có: \(\widehat {MHB} = \widehat {HBN} = \widehat {MNB} = {90^o}\) nên tứ giác HBNM là hình chữ nhật, do đó \(HB = MN = h\).
Tam giác HBM vuông tại H nên \(HB = MH.\tan \beta \), suy ra \(MH = \frac{{HB}}{{\tan \beta }} = \frac{h}{{\tan \beta }}\).
Tam giác MHA vuông tại H nên
\(HA = MH.\tan \alpha = \frac{h}{{\tan \beta }}.\tan \alpha \).
Ta có:
\(AB = HA + HB = \frac{h}{{\tan \beta }}.\tan \alpha + h = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\) (đpcm).
Trả lời câu hỏi Hoạt động 3 trang 96 SGK Toán 9 Cùng khám phá
Đo chiều cao cột cờ
Học sinh thực hiện ngoài trời và trình bày kết quả trước cả lớp.
Sử dụng giác kế và thước để đo góc nâng \(\alpha \) của đỉnh cột cờ, góc hạ \(\beta \) của chân cột cờ và chiều cao h tính từ mắt bạn quan sát đến mặt đất.
Điền các kết quả đo được vào Bảng 4.4 và tính chiều cao cột AB bằng công thức có được từ hoạt động 2.
Thực hiện nhiều lần với các bạn khác nhau và vị trí quan sát khác nhau. So sánh các kết quả tính và nhận xét.

Phương pháp giải:
+ Thực hiện đo góc nâng \(\alpha \) của đỉnh cột cờ, góc hạ \(\beta \) của chân cột cờ và chiều cao h tính từ mắt bạn quan sát đến mặt đất.5/8/2024
+ Áp dụng công thức \(AB = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\) để tính chiều cao cột cờ rồi điền vào bảng.
Lời giải chi tiết:

Các kết quả đo ở các lần là xấp xỉ nhau.
Trang 95 và 96 SGK Toán 9 tập 1 tập trung vào các bài tập liên quan đến hàm số bậc nhất và ứng dụng của nó. Các bài tập này thường yêu cầu học sinh vận dụng kiến thức về dạng tổng quát của hàm số bậc nhất (y = ax + b), các tính chất của hàm số (hệ số a, điểm thuộc đồ thị), và cách xác định hàm số khi biết các yếu tố khác nhau.
Bài tập này yêu cầu học sinh xác định hệ số a của hàm số y = ax + b khi biết một điểm thuộc đồ thị hàm số. Để giải bài tập này, học sinh cần thay tọa độ của điểm đã cho vào phương trình hàm số và giải phương trình để tìm ra giá trị của a.
Ví dụ: Cho hàm số y = ax + 2 và điểm A(1; 5) thuộc đồ thị hàm số. Tìm giá trị của a.
Giải:
Bài tập này yêu cầu học sinh xác định hàm số y = ax + b khi biết hai điểm thuộc đồ thị hàm số. Để giải bài tập này, học sinh cần thay tọa độ của hai điểm đã cho vào phương trình hàm số, tạo thành một hệ phương trình hai ẩn a và b, sau đó giải hệ phương trình để tìm ra giá trị của a và b.
Ví dụ: Cho hai điểm A(0; -1) và B(2; 3) thuộc đồ thị hàm số y = ax + b. Tìm giá trị của a và b.
Giải:
Các bài tập ứng dụng thường yêu cầu học sinh xây dựng hàm số bậc nhất mô tả một tình huống thực tế, sau đó sử dụng hàm số này để giải quyết các vấn đề liên quan. Ví dụ, bài toán về quãng đường đi được của một vật chuyển động đều, hoặc bài toán về chi phí sản xuất.
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Hãy viết hàm số biểu thị mối quan hệ giữa x và y.
Giải:
Quãng đường đi được bằng vận tốc nhân với thời gian. Vậy, y = 15x.
Ngoài SGK Toán 9 tập 1, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải các bài tập trang 95, 96 SGK Toán 9 tập 1 đòi hỏi học sinh phải nắm vững kiến thức về hàm số bậc nhất và ứng dụng của nó. Bằng cách luyện tập thường xuyên và áp dụng các kỹ năng giải bài tập, học sinh có thể tự tin giải quyết mọi bài toán và đạt kết quả tốt trong môn Toán.