Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 3, 4, 5 của sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi. Hãy cùng nhau khám phá và chinh phục những bài toán thú vị này nhé!
a) Cho hàm số \(y = \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.2 Đánh dấu các điểm (x;y) trong Bảng 6.2 trên mặt phẳng toạ độ. b) Cho hàm số \(y = - \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.3
Trả lời câu hỏi Hoạt động 3 trang 4 SGK Toán 9 Cùng khám phá
Quan sát đồ thị của hai hàm số \(y = \frac{1}{2}{x^2}\) (Hình 6.1a) và \(y = - \frac{1}{2}{x^2}\) (Hình 6.1b).
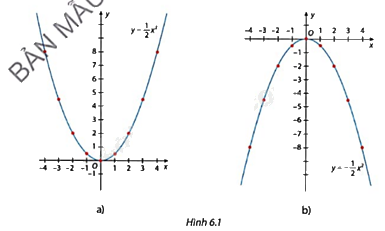
Với mỗi đồ thị, hãy đồ thị:
a) Đồ thị nằm phía trên hay phía dưới trục hoành;
b) Điểm thấp nhất hoặc điểm cao nhất của đồ thị;
c) Mối liên hệ giữa tung độ của hai điểm có hoành độ đối nhau thuộc đồ thị;
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy có trùng nhau hay không.
Phương pháp giải:
Nhìn vào đồ thị và nhận xét.
Lời giải chi tiết:
Với đồ thị \(y = \frac{1}{2}{x^2}\):
a) Đồ thị nằm phía trên trục hoành.
b) Điểm thấp nhất đồ thị là O(0;0)
c) Tung độ đối xứng với nhau qua trục Oy của hai điểm có hoành độ đối nhau thuộc đồ thị
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy trùng nhau.
Với đồ thị \(y = - \frac{1}{2}{x^2}\):
a) Đồ thị nằm phía dưới trục hoành.
b) Điểm thấp cao đồ thị là O(0;0)
c) Tung độ đối xứng với nhau qua trục Oy của hai điểm có hoành độ đối nhau thuộc đồ thị
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy trùng nhau.
Trả lời câu hỏi Vận dụng 2 trang 5SGK Toán 9 Cùng khám phá
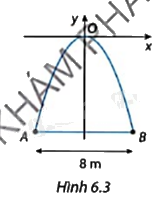
Một cổng chào được thiết kế theo hình parabol là một phần của đồ thị hàm số \(y = - \frac{{{x^2}}}{2}\). Khoảng cách giữa hai chân cổng là AB = 8 m (Hình 6.3).
a) Tìm hoành độ của hai điểm A, B.
b) Tìm chiều cao của cổng.
Phương pháp giải:
Từ khoảng cách AB = 8 suy ra hoành độ x.
Chiều cao của cổng chính là tung độ y.
Thay x vào \(y = - \frac{{{x^2}}}{2}\) để tìm y.
Lời giải chi tiết:
a) Khoảng cách AB = 8 nên OA = OB = \(\frac{{AB}}{2} = \frac{8}{2} = 4\).
Vậy hoành độ điểm B là 4, hoành độ điểm A là – 4
b) Thay x = 4 vào \(y = - \frac{{{x^2}}}{2}\) ta có: \( - \frac{{{4^2}}}{2} = - 8\).
Vậy chiều cao của cổng là 8 m.
Trả lời câu hỏi Luyện tập 2 trang 5 SGK Toán 9 Cùng khám phá
Vẽ đồ thị y = -2x2.
Phương pháp giải:
Cách vẽ đồ thị \(y = a{x^2}\left( {a \ne 0} \right)\) như sau:
- Vẽ hệ trục toạ độ Oxy.
- Lập bảng một số giá trị tương ứng của x và y. Đánh dấu các điểm tương ứng trên mặt phẳng toạ độ. Ta thường lấy điểm O và những điểm có hoành độ đối nhau.
- Vẽ đường thẳng parabol đi qua các điểm vừa đánh dấu.
Lời giải chi tiết:
Bảng một số giá trị tương ứng x và y:

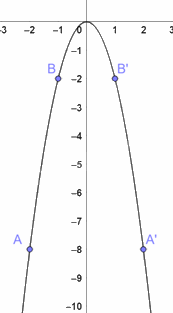
Trên mặt phẳng toạ độ, đánh dấu các điểm A(-2;-8), B(-1;-2), O(0;0), B’(1;-2), A’(2; -8).
Đồ thị hàm số y = -2x2 là đường parabol đi qua năm điểm A, B, O, B’, A’.
Trả lời câu hỏi Hoạt động 2 trang 3 SGK Toán 9 Cùng khám phá
a) Cho hàm số \(y = \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.2
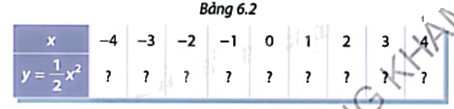
Đánh dấu các điểm (x;y) trong Bảng 6.2 trên mặt phẳng toạ độ.
b) Cho hàm số \(y = - \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.3
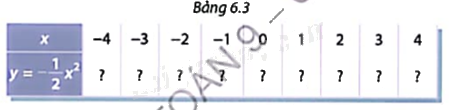
Phương pháp giải:
Thay lần lượt giá x vào hàm số \(y = \frac{1}{2}{x^2}\) và \(y = - \frac{1}{2}{x^2}\) để tính y.
Đánh dấu các điểm trên mặt phẳng toạ độ.
Lời giải chi tiết:
a)

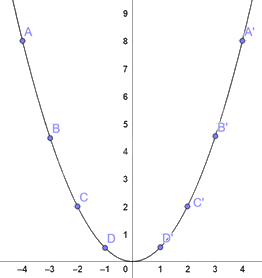
Lấy các điểm A(-4;8), B(-3; \(\frac{9}{2}\)), C(-2;2), D(-1; \(\frac{1}{2}\)), O(0;0), A’(4;8), B’(3; \(\frac{9}{2}\)),
C’(2;2), D’(1; \(\frac{1}{2}\)) trên mặt phẳng toạ độ tạo một đường cong bên dưới.
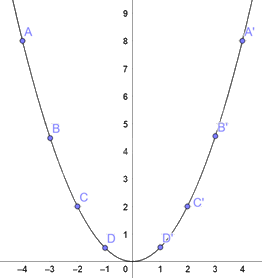
b)

Trả lời câu hỏi Hoạt động 2 trang 3 SGK Toán 9 Cùng khám phá
a) Cho hàm số \(y = \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.2
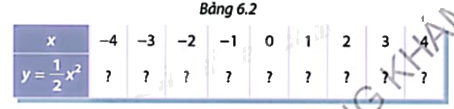
Đánh dấu các điểm (x;y) trong Bảng 6.2 trên mặt phẳng toạ độ.
b) Cho hàm số \(y = - \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.3
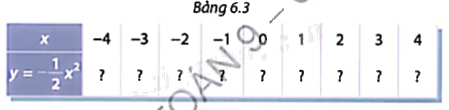
Phương pháp giải:
Thay lần lượt giá x vào hàm số \(y = \frac{1}{2}{x^2}\) và \(y = - \frac{1}{2}{x^2}\) để tính y.
Đánh dấu các điểm trên mặt phẳng toạ độ.
Lời giải chi tiết:
a)

Lấy các điểm A(-4;8), B(-3; \(\frac{9}{2}\)), C(-2;2), D(-1; \(\frac{1}{2}\)), O(0;0), A’(4;8), B’(3; \(\frac{9}{2}\)),
C’(2;2), D’(1; \(\frac{1}{2}\)) trên mặt phẳng toạ độ tạo một đường cong bên dưới.
b)

Trả lời câu hỏi Hoạt động 3 trang 4 SGK Toán 9 Cùng khám phá
Quan sát đồ thị của hai hàm số \(y = \frac{1}{2}{x^2}\) (Hình 6.1a) và \(y = - \frac{1}{2}{x^2}\) (Hình 6.1b).
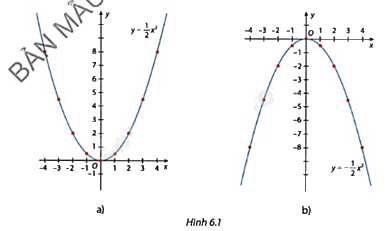
Với mỗi đồ thị, hãy đồ thị:
a) Đồ thị nằm phía trên hay phía dưới trục hoành;
b) Điểm thấp nhất hoặc điểm cao nhất của đồ thị;
c) Mối liên hệ giữa tung độ của hai điểm có hoành độ đối nhau thuộc đồ thị;
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy có trùng nhau hay không.
Phương pháp giải:
Nhìn vào đồ thị và nhận xét.
Lời giải chi tiết:
Với đồ thị \(y = \frac{1}{2}{x^2}\):
a) Đồ thị nằm phía trên trục hoành.
b) Điểm thấp nhất đồ thị là O(0;0)
c) Tung độ đối xứng với nhau qua trục Oy của hai điểm có hoành độ đối nhau thuộc đồ thị
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy trùng nhau.
Với đồ thị \(y = - \frac{1}{2}{x^2}\):
a) Đồ thị nằm phía dưới trục hoành.
b) Điểm thấp cao đồ thị là O(0;0)
c) Tung độ đối xứng với nhau qua trục Oy của hai điểm có hoành độ đối nhau thuộc đồ thị
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy trùng nhau.
Trả lời câu hỏi Luyện tập 2 trang 5 SGK Toán 9 Cùng khám phá
Vẽ đồ thị y = -2x2.
Phương pháp giải:
Cách vẽ đồ thị \(y = a{x^2}\left( {a \ne 0} \right)\) như sau:
- Vẽ hệ trục toạ độ Oxy.
- Lập bảng một số giá trị tương ứng của x và y. Đánh dấu các điểm tương ứng trên mặt phẳng toạ độ. Ta thường lấy điểm O và những điểm có hoành độ đối nhau.
- Vẽ đường thẳng parabol đi qua các điểm vừa đánh dấu.
Lời giải chi tiết:
Bảng một số giá trị tương ứng x và y:

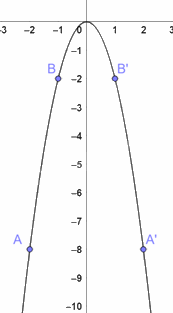
Trên mặt phẳng toạ độ, đánh dấu các điểm A(-2;-8), B(-1;-2), O(0;0), B’(1;-2), A’(2; -8).
Đồ thị hàm số y = -2x2 là đường parabol đi qua năm điểm A, B, O, B’, A’.
Trả lời câu hỏi Vận dụng 2 trang 5SGK Toán 9 Cùng khám phá
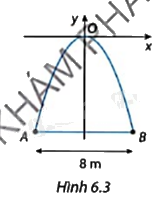
Một cổng chào được thiết kế theo hình parabol là một phần của đồ thị hàm số \(y = - \frac{{{x^2}}}{2}\). Khoảng cách giữa hai chân cổng là AB = 8 m (Hình 6.3).
a) Tìm hoành độ của hai điểm A, B.
b) Tìm chiều cao của cổng.
Phương pháp giải:
Từ khoảng cách AB = 8 suy ra hoành độ x.
Chiều cao của cổng chính là tung độ y.
Thay x vào \(y = - \frac{{{x^2}}}{2}\) để tìm y.
Lời giải chi tiết:
a) Khoảng cách AB = 8 nên OA = OB = \(\frac{{AB}}{2} = \frac{8}{2} = 4\).
Vậy hoành độ điểm B là 4, hoành độ điểm A là – 4
b) Thay x = 4 vào \(y = - \frac{{{x^2}}}{2}\) ta có: \( - \frac{{{4^2}}}{2} = - 8\).
Vậy chiều cao của cổng là 8 m.
Mục 2 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để tìm ra lời giải chính xác.
Bài 1 thường là bài tập áp dụng trực tiếp các kiến thức lý thuyết đã học. Để giải bài này, học sinh cần xác định đúng các yếu tố cần tìm và sử dụng công thức phù hợp. Ví dụ, nếu bài tập liên quan đến phương trình bậc hai, học sinh cần nhớ công thức nghiệm và cách tính delta.
Bài 2 có thể là bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học và kết hợp với các kỹ năng tư duy logic. Trong trường hợp này, học sinh có thể cần phải phân tích đề bài một cách kỹ lưỡng, tìm ra mối liên hệ giữa các yếu tố và xây dựng một phương án giải phù hợp.
Bài 3 thường là bài tập tổng hợp, yêu cầu học sinh phải sử dụng nhiều kiến thức và kỹ năng khác nhau để giải quyết. Để giải bài này, học sinh cần phải có một cái nhìn tổng quan về toàn bộ chủ đề và biết cách kết hợp các kiến thức đã học một cách hiệu quả.
Bài tập: Giải phương trình 2x2 - 5x + 2 = 0
Lời giải:
Kết luận: Phương trình có hai nghiệm là x1 = 2 và x2 = 0.5
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh nên tự giải thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 3, 4, 5 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao!