Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 115, 116, 117 sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Ta chép lại dưới đây Bảng 10.19 về chiều cao của 40 học sinh. Nhóm mặc đồng phục cỡ M (ứng với chiều cao từ 152 cm đến dưới 158 cm) chiếm bao nhiêu phần trăm trong tổng số 40 học sinh? Hãy trình bày cách tìm kết quả.
Trả lời câu hỏi Hoạt động 2 trang 115 SGK Toán 9 Cùng khám phá
Ta chép lại dưới đây Bảng 10.19 về chiều cao của 40 học sinh. Nhóm mặc đồng phục cỡ M (ứng với chiều cao từ 152 cm đến dưới 158 cm) chiếm bao nhiêu phần trăm trong tổng số 40 học sinh? Hãy trình bày cách tìm kết quả.

Phương pháp giải:
Áp dụng công thức: Số HS mặc đồng phục cỡ M chia cho tổng số 40 học sinh.
Lời giải chi tiết:
Áp dụng công thức: Số HS mặc đồng phục cỡ M chia cho tổng số 40 học sinh nhân 100%.
Ta có \(\frac{{18}}{{40}} = 0,45 = 45\% \).
Trả lời câu hỏi Luyện tập 2 trang 117SGK Toán 9 Cùng khám phá
Một cửa hàng điện máy ghi lại lợi nhuận thu được trong một số ngày ở bảng sau:

a) Lập bảng tần số - tần số tương đối ghép nhóm với các nhóm ghép [5;6), [6;7), [7;8), [8;9).
b) Dựa vào bảng lập được, hãy đưa ra nhận xét về lợi nhuận hằng ngày của cửa hàng.
Phương pháp giải:
Bảng tần số - tần số tương đối ghép nhóm là bảng có cả tần số ghép nhóm và tần số tương đối ghép nhóm.
Dựa vào bảng tần số - tần số tương đối ghép nhóm để nhận xét.
Lời giải chi tiết:
a) Bảng tần số - tần số tương đối ghép nhóm

b) Lợi nhuận hằng ngày của cửa hàng nhiều nhất khoảng 7 đến 8 triệu đồng.
Trả lời câu hỏi Vận dụng trang 117 SGK Toán 9 Cùng khám phá
Trở lại với tình huống đo chiều cao của 40 học sinh để đặt may quần áo thể thao cho toàn trường (Hoạt động 1)
Hoạt động 1: Kết quả đo chiều cao của 40 học sinh được thống kê trong bảng sau:
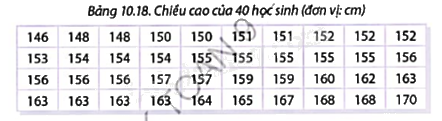
Theo quy định của công ty may mặc, cỡ S tương ứng với chiều cao từ 146 cm đến dưới 152 cm. Cỡ M ứng với chiều cao từ 152 cm đến dưới 158 cm. Cỡ L tương ứng với chiều cao từ 158 cm đến dưới 164 cm. Cỡ XL ứng với chiều cao từ 164 cm đến 170 cm.
Nếu 40 học sinh có chiều cao đại diện được cho học sinh toàn trường thì số quần áo cần may ở mỗi kích cỡ cho toàn thể học sinh của trường là bao nhiêu, biết rằng trường có 1200 học sinh?
Phương pháp giải:
Bảng tần số - tần số tương đối ghép nhóm là bảng có cả tần số ghép nhóm và tần số tương đối ghép nhóm của 40 học sinh
Dựa tần số tương đối của 40 học sinh để suy ra tìm từng loại số nhóm học sinh mặc áo cỡ S, M, L, XL.
Lời giải chi tiết:
Bảng tần số - tần số tương đối ghép nhóm
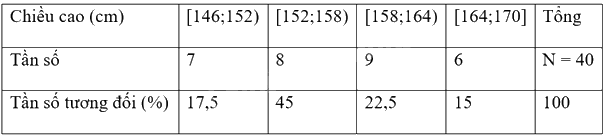
Gọi nhóm số học sinh mặc cỡ S là k
Ta có tần số tương đối là \(\frac{k}{{120}}.100\% = 17,5\% \) suy ra \(k = \frac{{17,5.1200}}{{100}} = 210\) học sinh.
Gọi nhóm số học sinh mặc cỡ M là h
Ta có tần số tương đối là \(\frac{h}{{120}}.100\% = 45\% \) suy ra \(k = \frac{{45.1200}}{{100}} = 540\) học sinh.
Gọi nhóm số học sinh mặc cỡ L là l
Ta có tần số tương đối là \(\frac{l}{{120}}.100\% = 22,5\% \) suy ra \(k = \frac{{22,5.1200}}{{100}} = 270\) học sinh.
Gọi nhóm số học sinh mặc cỡ XL là m
Ta có tần số tương đối là \(\frac{m}{{120}}.100\% = 15\% \) suy ra \(k = \frac{{15.1200}}{{100}} = 180\) học sinh.
Trả lời câu hỏi Hoạt động 2 trang 115 SGK Toán 9 Cùng khám phá
Ta chép lại dưới đây Bảng 10.19 về chiều cao của 40 học sinh. Nhóm mặc đồng phục cỡ M (ứng với chiều cao từ 152 cm đến dưới 158 cm) chiếm bao nhiêu phần trăm trong tổng số 40 học sinh? Hãy trình bày cách tìm kết quả.

Phương pháp giải:
Áp dụng công thức: Số HS mặc đồng phục cỡ M chia cho tổng số 40 học sinh.
Lời giải chi tiết:
Áp dụng công thức: Số HS mặc đồng phục cỡ M chia cho tổng số 40 học sinh nhân 100%.
Ta có \(\frac{{18}}{{40}} = 0,45 = 45\% \).
Trả lời câu hỏi Luyện tập 2 trang 117SGK Toán 9 Cùng khám phá
Một cửa hàng điện máy ghi lại lợi nhuận thu được trong một số ngày ở bảng sau:

a) Lập bảng tần số - tần số tương đối ghép nhóm với các nhóm ghép [5;6), [6;7), [7;8), [8;9).
b) Dựa vào bảng lập được, hãy đưa ra nhận xét về lợi nhuận hằng ngày của cửa hàng.
Phương pháp giải:
Bảng tần số - tần số tương đối ghép nhóm là bảng có cả tần số ghép nhóm và tần số tương đối ghép nhóm.
Dựa vào bảng tần số - tần số tương đối ghép nhóm để nhận xét.
Lời giải chi tiết:
a) Bảng tần số - tần số tương đối ghép nhóm

b) Lợi nhuận hằng ngày của cửa hàng nhiều nhất khoảng 7 đến 8 triệu đồng.
Trả lời câu hỏi Vận dụng trang 117 SGK Toán 9 Cùng khám phá
Trở lại với tình huống đo chiều cao của 40 học sinh để đặt may quần áo thể thao cho toàn trường (Hoạt động 1)
Hoạt động 1: Kết quả đo chiều cao của 40 học sinh được thống kê trong bảng sau:
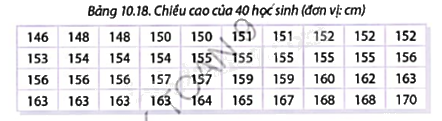
Theo quy định của công ty may mặc, cỡ S tương ứng với chiều cao từ 146 cm đến dưới 152 cm. Cỡ M ứng với chiều cao từ 152 cm đến dưới 158 cm. Cỡ L tương ứng với chiều cao từ 158 cm đến dưới 164 cm. Cỡ XL ứng với chiều cao từ 164 cm đến 170 cm.
Nếu 40 học sinh có chiều cao đại diện được cho học sinh toàn trường thì số quần áo cần may ở mỗi kích cỡ cho toàn thể học sinh của trường là bao nhiêu, biết rằng trường có 1200 học sinh?
Phương pháp giải:
Bảng tần số - tần số tương đối ghép nhóm là bảng có cả tần số ghép nhóm và tần số tương đối ghép nhóm của 40 học sinh
Dựa tần số tương đối của 40 học sinh để suy ra tìm từng loại số nhóm học sinh mặc áo cỡ S, M, L, XL.
Lời giải chi tiết:
Bảng tần số - tần số tương đối ghép nhóm
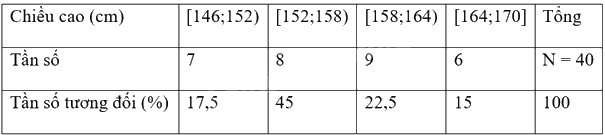
Gọi nhóm số học sinh mặc cỡ S là k
Ta có tần số tương đối là \(\frac{k}{{120}}.100\% = 17,5\% \) suy ra \(k = \frac{{17,5.1200}}{{100}} = 210\) học sinh.
Gọi nhóm số học sinh mặc cỡ M là h
Ta có tần số tương đối là \(\frac{h}{{120}}.100\% = 45\% \) suy ra \(k = \frac{{45.1200}}{{100}} = 540\) học sinh.
Gọi nhóm số học sinh mặc cỡ L là l
Ta có tần số tương đối là \(\frac{l}{{120}}.100\% = 22,5\% \) suy ra \(k = \frac{{22,5.1200}}{{100}} = 270\) học sinh.
Gọi nhóm số học sinh mặc cỡ XL là m
Ta có tần số tương đối là \(\frac{m}{{120}}.100\% = 15\% \) suy ra \(k = \frac{{15.1200}}{{100}} = 180\) học sinh.
Mục 2 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề cụ thể trong hình học hoặc đại số. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của bài toán và áp dụng đúng phương pháp giải là yếu tố then chốt để đạt được kết quả tốt.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến hàm số bậc nhất). Để giải bài tập này, ta cần xác định hệ số góc và tung độ gốc của hàm số, sau đó sử dụng các tính chất của hàm số để tìm ra đáp án.
Bài tập này có thể liên quan đến việc... (giả sử bài tập liên quan đến hệ phương trình). Để giải bài tập này, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Việc lựa chọn phương pháp phù hợp sẽ giúp ta giải bài tập một cách nhanh chóng và chính xác.
Bài tập này thường yêu cầu học sinh... (giả sử bài tập liên quan đến tam giác đồng dạng). Để giải bài tập này, ta cần chứng minh hai tam giác đồng dạng dựa trên các tiêu chuẩn đồng dạng đã học. Sau khi chứng minh được hai tam giác đồng dạng, ta có thể sử dụng các tỉ lệ tương ứng để tìm ra đáp án.
Để giải bài tập Toán 9 một cách hiệu quả, học sinh cần:
Trong quá trình giải bài tập, học sinh cần chú ý đến các đơn vị đo lường, các dấu âm và dương, và các điều kiện của bài toán. Việc mắc lỗi trong các chi tiết nhỏ có thể dẫn đến kết quả sai.
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải các bài tập trong mục 2 trang 115, 116, 117 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt được kết quả cao trong môn Toán!
| Bài tập | Chủ đề | Phương pháp giải |
|---|---|---|
| Bài tập 1 | Hàm số bậc nhất | Xác định hệ số góc và tung độ gốc |
| Bài tập 2 | Hệ phương trình | Phương pháp thế hoặc cộng đại số |
| Bài tập 3 | Tam giác đồng dạng | Chứng minh tam giác đồng dạng và sử dụng tỉ lệ tương ứng |