Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 77, 78, 79 của sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Hãy chỉ ra các vật thể có dạng hình cầu trong Hình 9.33.
Trả lời câu hỏi Luyện tập 1 trang 79SGK Toán 9 Cùng khám phá
Cho hình cầu tâm I đường kính 1 dm. Khi cắt hình cầu trên bởi một mặt phẳng ta được một hình tròn có chu vi \(\frac{\pi }{2}\)dm. Mặt phẳng đó có đi qua tâm I của mặt cầu không? Vì sao?
Phương pháp giải:
Nếu mặt phẳng cắt mặt cầu đi qua tâm O thì đường tròn có bán kính bằng R. Đây được gọi là đường tròn lớn.
Lời giải chi tiết:
Ta có chu vi hình tròn là C = \(\pi d = \frac{\pi }{2}\).
Suy ra D = \(\frac{1}{2}\) hay R = \(\frac{1}{4}\).
Mặt phẳng đó không đi qua tâm I của mặt cầu vì có mặt cắt là hình tròn có bán kính không bằng bán kính tâm I.
Trả lời câu hỏi Hoạt động 2 trang 78SGK Toán 9 Cùng khám phá
Quan sát Hình 9.35, hãy cho biết khi bổ quả cam có dạng hình cầu thì mặt cắt của quả cam có dạng hình gì.

Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Mặt cắt của quả cam có dạng hình tròn.
Trả lời câu hỏi Hoạt động 1 trang 77SGK Toán 9 Cùng khám phá
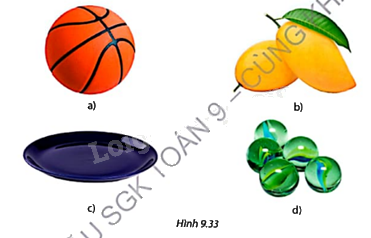
Hãy chỉ ra các vật thể có dạng hình cầu trong Hình 9.33.
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Các vật thể có dạng hình cầu là a và d.
Trả lời câu hỏi Vận dụng 1 trang 79SGK Toán 9 Cùng khám phá
Trái Đất được xem như một hình cầu với bán kính khoảng 6371 km. Nếu coi xích đạo là đường tròn lớn của hình cầu này thì độ dài đường xích đạo là bao nhiêu kilomet?

Phương pháp giải:
Nếu mặt phẳng cắt mặt cầu đi qua tâm O thì đường tròn có bán kính bằng R. Đây được gọi là đường tròn lớn.
Lời giải chi tiết:
Nếu coi xích đạo là đường tròn lớn của hình cầu này thì độ dài đường xích đạo là 6371 km.
Trả lời câu hỏi Hoạt động 1 trang 77SGK Toán 9 Cùng khám phá
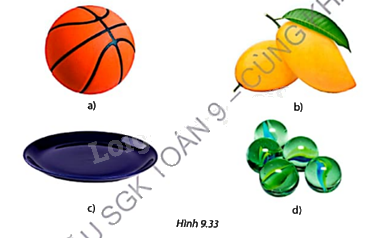
Hãy chỉ ra các vật thể có dạng hình cầu trong Hình 9.33.
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Các vật thể có dạng hình cầu là a và d.
Trả lời câu hỏi Hoạt động 2 trang 78SGK Toán 9 Cùng khám phá
Quan sát Hình 9.35, hãy cho biết khi bổ quả cam có dạng hình cầu thì mặt cắt của quả cam có dạng hình gì.

Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Mặt cắt của quả cam có dạng hình tròn.
Trả lời câu hỏi Luyện tập 1 trang 79SGK Toán 9 Cùng khám phá
Cho hình cầu tâm I đường kính 1 dm. Khi cắt hình cầu trên bởi một mặt phẳng ta được một hình tròn có chu vi \(\frac{\pi }{2}\)dm. Mặt phẳng đó có đi qua tâm I của mặt cầu không? Vì sao?
Phương pháp giải:
Nếu mặt phẳng cắt mặt cầu đi qua tâm O thì đường tròn có bán kính bằng R. Đây được gọi là đường tròn lớn.
Lời giải chi tiết:
Ta có chu vi hình tròn là C = \(\pi d = \frac{\pi }{2}\).
Suy ra D = \(\frac{1}{2}\) hay R = \(\frac{1}{4}\).
Mặt phẳng đó không đi qua tâm I của mặt cầu vì có mặt cắt là hình tròn có bán kính không bằng bán kính tâm I.
Trả lời câu hỏi Vận dụng 1 trang 79SGK Toán 9 Cùng khám phá
Trái Đất được xem như một hình cầu với bán kính khoảng 6371 km. Nếu coi xích đạo là đường tròn lớn của hình cầu này thì độ dài đường xích đạo là bao nhiêu kilomet?

Phương pháp giải:
Nếu mặt phẳng cắt mặt cầu đi qua tâm O thì đường tròn có bán kính bằng R. Đây được gọi là đường tròn lớn.
Lời giải chi tiết:
Nếu coi xích đạo là đường tròn lớn của hình cầu này thì độ dài đường xích đạo là 6371 km.
Mục 1 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề cụ thể, ví dụ như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, hoặc các ứng dụng của phương trình bậc hai. Việc nắm vững kiến thức nền tảng và phương pháp giải bài tập trong mục này là rất quan trọng để học tốt các kiến thức tiếp theo.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 77, 78, 79, chúng ta sẽ đi vào giải chi tiết từng bài tập. Lưu ý rằng, trước khi bắt đầu giải bài tập, các em nên đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
(Giả sử bài 1 yêu cầu giải một phương trình bậc nhất)
Để giải phương trình bậc nhất, ta thực hiện các bước sau:
Ví dụ: Giải phương trình 2x + 5 = 11
Bước 1: 2x + 5 = 11
Bước 2: 2x = 11 - 5 = 6
Bước 3: x = 6 / 2 = 3
Vậy nghiệm của phương trình là x = 3
(Giả sử bài 2 yêu cầu giải một hệ phương trình bậc nhất hai ẩn)
Có nhiều phương pháp để giải hệ phương trình bậc nhất hai ẩn, ví dụ như phương pháp thế, phương pháp cộng đại số, hoặc phương pháp ma trận. Tùy thuộc vào từng hệ phương trình cụ thể, ta có thể lựa chọn phương pháp phù hợp nhất.
Ví dụ: Giải hệ phương trình sau:
x + y = 5
2x - y = 1
Sử dụng phương pháp cộng đại số, ta có:
(x + y) + (2x - y) = 5 + 1
3x = 6
x = 2
Thay x = 2 vào phương trình x + y = 5, ta có:
2 + y = 5
y = 3
Vậy nghiệm của hệ phương trình là x = 2, y = 3
(Giả sử bài 3 yêu cầu ứng dụng phương trình bậc hai để giải một bài toán thực tế)
Khi giải các bài toán ứng dụng, điều quan trọng là phải hiểu rõ đề bài, xác định các đại lượng liên quan và thiết lập phương trình bậc hai phù hợp. Sau khi giải phương trình, ta cần kiểm tra xem nghiệm có phù hợp với điều kiện thực tế của bài toán hay không.
Hy vọng rằng, với những hướng dẫn chi tiết và dễ hiểu trên đây, các em sẽ tự tin hơn trong việc giải các bài tập trong mục 1 trang 77, 78, 79 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 (Trang 77) | Giải phương trình bậc nhất |
| Bài 2 (Trang 78) | Giải hệ phương trình bậc nhất hai ẩn |
| Bài 3 (Trang 79) | Ứng dụng phương trình bậc hai |