Chào mừng các em học sinh đến với bài giải bài tập 8.7 trang 54 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học về phương trình bậc hai một ẩn.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Ngoài ra, chúng tôi còn có các bài giảng video, bài tập luyện tập và các tài liệu học tập khác để hỗ trợ các em học toán hiệu quả hơn.
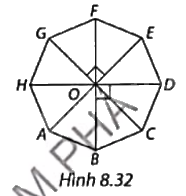
Cho bát giác đều ABCDEFGH như Hình 8.32. Biết điểm O cách đều các đỉnh của bát giác đều. a) Tìm ảnh của tam giác OAB qua phép quay ngược chiều 180o tâm O. b) Tìm ảnh của bát giác đều qua phép quay thuận chiều 90o tâm O và nhận xét. c) Tìm ba phép quay tâm O giữ nguyên bát giác đều này.
Đề bài
Cho bát giác đều ABCDEFGH như Hình 8.32. Biết điểm O cách đều các đỉnh của bát giác đều.
a) Tìm ảnh của tam giác OAB qua phép quay ngược chiều 180o tâm O.
b) Tìm ảnh của bát giác đều qua phép quay thuận chiều 90o tâm O và nhận xét.
c) Tìm ba phép quay tâm O giữ nguyên bát giác đều này.
Phương pháp giải - Xem chi tiết
Phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O;OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OA’ thì điểm A tạo nên cung AmA’ có số đo \({\alpha ^o}\)
(Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O).
Lời giải chi tiết
Ta có AB = BC = CD = DE = EF = FG = GH = HA nên số đo các cung nhỏ AB, BC, CD, DE, EF, FG, GH, HA đều bằng \(\frac{{{{360}^o}}}{8} = {45^o}\).
a) Vì \(\widehat {AOB} = {45^o}\) nên số đo cung nhỏ AB bằng 45o. Suy ra ảnh tam giác OAB qua phép quay ngược chiều 180o tâm O là tam giác OEF.
b) Ảnh của bát giác đều ABCDEFGH qua phép quay thuận chiều 90o tâm O là bát giác đều CDEFGHAB.
c) Ba phép quay tâm O giữ nguyên bát giác đều này là \({45^o};{90^o};{135^o}\).
Bài tập 8.7 trang 54 SGK Toán 9 tập 2 yêu cầu giải các phương trình bậc hai một ẩn. Để giải quyết bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về phương trình bậc hai, bao gồm:
Để giải bài tập 8.7, chúng ta sẽ áp dụng các kiến thức trên để giải từng phương trình cụ thể. Dưới đây là hướng dẫn chi tiết cho từng phương trình:
Bước 1: Xác định các hệ số a, b, c:
Bước 2: Tính Δ:
Δ = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Bước 3: Tính nghiệm:
x = (-b ± √Δ) / 2a = (5 ± √9) / (2 * 2) = (5 ± 3) / 4
Vậy, phương trình có hai nghiệm phân biệt:
Bước 1: Xác định các hệ số a, b, c:
Bước 2: Tính Δ:
Δ = b2 - 4ac = (-4)2 - 4 * 1 * 4 = 16 - 16 = 0
Bước 3: Tính nghiệm:
x = -b / 2a = -(-4) / (2 * 1) = 4 / 2 = 2
Vậy, phương trình có nghiệm kép x = 2
Bước 1: Xác định các hệ số a, b, c:
Bước 2: Tính Δ:
Δ = b2 - 4ac = (2)2 - 4 * 3 * 1 = 4 - 12 = -8
Bước 3: Kết luận:
Vì Δ < 0, phương trình vô nghiệm.
Phương trình bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về phương trình bậc hai, các em có thể làm thêm các bài tập sau:
Hy vọng bài giải này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 8.7 trang 54 SGK Toán 9 tập 2. Chúc các em học tập tốt!