Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 100, 101, 102 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Trong Hình 5.7, khung cửa sổ có dạng hình tròn. Đầu mút của thanh song cửa AB nằm trên đường nào?
Trả lời câu hỏi Hoạt động 4 trang 101SGK Toán 9 Cùng khám phá
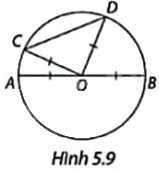
Trong Hình 5.9,lần lượt so sánh độ dài dây CD, đường kính AB với tổng độ dài \(OC + OD\), em hãy cho biết trong hai dây AB và CD, dây nào dài hơn?
Phương pháp giải:
+ Vì 4 điểm A, B, C, D thuộc (O) nên \(OA = OB = OC = OD\). Do đó, \(OC + OD = OA + OB = AB\).
+ Áp dụng bất đẳng thức tam giác vào tam giác OCD ta có: \(OC + OD > CD\), từ đó so sánh AB và CD.
Lời giải chi tiết:
Vì 4 điểm A, B, C, D thuộc (O) nên \(OA = OB = OC = OD\).
Do đó, \(OC + OD = OA + OB = AB\).
Trong tam giác OCD có: \(OC + OD > CD\) (bất đẳng thức trong tam giác).
Do đó, \(AB > CD\).
Trả lời câu hỏi Luyện tập 3 trang 100 SGK Toán 9 Cùng khám phá
Trên đường tròn (O), lấy bốn điểm M, N, P, Q phân biệt. Vẽ và nêu tên tất cả các dây của (O) có đầu mút là hai trong số bốn điểm trên.
Phương pháp giải:
Đoạn thẳng nối hai điểm phân biệt của đường tròn được gọi là một dây của đường tròn.
Lời giải chi tiết:
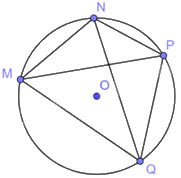
Các dây của (O) có đầu mút là hai trong số bốn điểm là: MN, NP, PQ, QM, NQ, MP.
Trả lời câu hỏi Vận dụng 2 trang 102 SGK Toán 9 Cùng khám phá
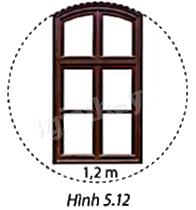
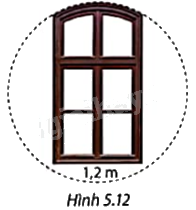
Cửa sổ được thiết kế với phần vòm bên trên là một phần của một đường tròn (Hình 5.12). Nếu chiều rộng cửa là 1,2m thì bán kính của đường tròn nói trên ít nhất bằng bao nhiêu mét?
Phương pháp giải:
Trong đường tròn, đường kính là dây lớn nhất.
Lời giải chi tiết:
Gọi d là đường kính của đường tròn, r là bán kính của đường tròn.
Vì chiều rộng cửa sổ là một dây của đường tròn nên \(d \ge 1,2m\).
Do đó, \(r \ge \frac{{1,2}}{2} = 0,6m\).
Vậy bán kính của đường tròn nói trên ít nhất bằng 0,6m.
Trả lời câu hỏi Luyện tập 4 trang 101SGK Toán 9 Cùng khám phá
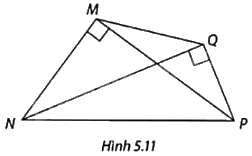
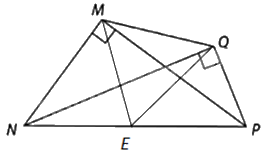
So sánh độ dài hai cạnh MQ và NP trong Hình 5.11.
Phương pháp giải:
+ Chứng minh 4 điểm M, N, P, Q cùng thuộc đường tròn đường kính NP.
+ Do đó, \(MQ \le NP\).
Lời giải chi tiết:
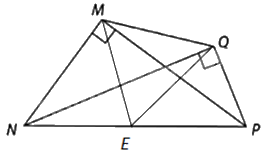
Gọi E là trung điểm của NP.
Vì tam giác MNP và tam giác NQP là các tam giác vuông có cùng cạnh huyền NP và ME, QE lần lượt là trung tuyến ứng với cạnh huyền NP nên \(ME = EQ = NE = EP\) (tính chất trung tuyến ứng với cạnh huyền). Do đó, M, Q thuộc đường tròn đường kính NP. Suy ra, \(MQ \le NP\).
Trả lời câu hỏi Hoạt động 3 trang 100SGK Toán 9 Cùng khám phá
Trong Hình 5.7, khung cửa sổ có dạng hình tròn. Đầu mút của thanh song cửa AB nằm trên đường nào?

Phương pháp giải:
Nhìn hình và rút ra nhận xét.
Lời giải chi tiết:
Đầu mút của thanh song cửa AB nằm trên khung cửa sổ.
Trả lời câu hỏi Hoạt động 3 trang 100SGK Toán 9 Cùng khám phá
Trong Hình 5.7, khung cửa sổ có dạng hình tròn. Đầu mút của thanh song cửa AB nằm trên đường nào?

Phương pháp giải:
Nhìn hình và rút ra nhận xét.
Lời giải chi tiết:
Đầu mút của thanh song cửa AB nằm trên khung cửa sổ.
Trả lời câu hỏi Luyện tập 3 trang 100 SGK Toán 9 Cùng khám phá
Trên đường tròn (O), lấy bốn điểm M, N, P, Q phân biệt. Vẽ và nêu tên tất cả các dây của (O) có đầu mút là hai trong số bốn điểm trên.
Phương pháp giải:
Đoạn thẳng nối hai điểm phân biệt của đường tròn được gọi là một dây của đường tròn.
Lời giải chi tiết:
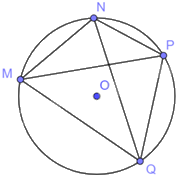
Các dây của (O) có đầu mút là hai trong số bốn điểm là: MN, NP, PQ, QM, NQ, MP.
Trả lời câu hỏi Hoạt động 4 trang 101SGK Toán 9 Cùng khám phá
Trong Hình 5.9,lần lượt so sánh độ dài dây CD, đường kính AB với tổng độ dài \(OC + OD\), em hãy cho biết trong hai dây AB và CD, dây nào dài hơn?
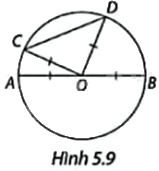
Phương pháp giải:
+ Vì 4 điểm A, B, C, D thuộc (O) nên \(OA = OB = OC = OD\). Do đó, \(OC + OD = OA + OB = AB\).
+ Áp dụng bất đẳng thức tam giác vào tam giác OCD ta có: \(OC + OD > CD\), từ đó so sánh AB và CD.
Lời giải chi tiết:
Vì 4 điểm A, B, C, D thuộc (O) nên \(OA = OB = OC = OD\).
Do đó, \(OC + OD = OA + OB = AB\).
Trong tam giác OCD có: \(OC + OD > CD\) (bất đẳng thức trong tam giác).
Do đó, \(AB > CD\).
Trả lời câu hỏi Luyện tập 4 trang 101SGK Toán 9 Cùng khám phá
So sánh độ dài hai cạnh MQ và NP trong Hình 5.11.
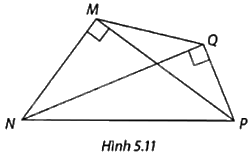
Phương pháp giải:
+ Chứng minh 4 điểm M, N, P, Q cùng thuộc đường tròn đường kính NP.
+ Do đó, \(MQ \le NP\).
Lời giải chi tiết:
Gọi E là trung điểm của NP.
Vì tam giác MNP và tam giác NQP là các tam giác vuông có cùng cạnh huyền NP và ME, QE lần lượt là trung tuyến ứng với cạnh huyền NP nên \(ME = EQ = NE = EP\) (tính chất trung tuyến ứng với cạnh huyền). Do đó, M, Q thuộc đường tròn đường kính NP. Suy ra, \(MQ \le NP\).
Trả lời câu hỏi Vận dụng 2 trang 102 SGK Toán 9 Cùng khám phá
Cửa sổ được thiết kế với phần vòm bên trên là một phần của một đường tròn (Hình 5.12). Nếu chiều rộng cửa là 1,2m thì bán kính của đường tròn nói trên ít nhất bằng bao nhiêu mét?
Phương pháp giải:
Trong đường tròn, đường kính là dây lớn nhất.
Lời giải chi tiết:
Gọi d là đường kính của đường tròn, r là bán kính của đường tròn.
Vì chiều rộng cửa sổ là một dây của đường tròn nên \(d \ge 1,2m\).
Do đó, \(r \ge \frac{{1,2}}{2} = 0,6m\).
Vậy bán kính của đường tròn nói trên ít nhất bằng 0,6m.
Mục 2 của chương trình Toán 9 tập 1 thường tập trung vào các chủ đề như hàm số bậc nhất, đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các chương tiếp theo.
Trang 100 thường chứa các bài tập về việc xác định hàm số bậc nhất, tìm hệ số góc và tung độ gốc. Các bài tập này giúp học sinh rèn luyện kỹ năng phân tích và hiểu rõ cấu trúc của hàm số.
Bài 1: Cho hàm số y = 2x + 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Giải:
Trang 101 thường tập trung vào việc vẽ đồ thị hàm số bậc nhất và xác định các điểm thuộc đồ thị. Đây là bước quan trọng để học sinh hình dung được mối quan hệ giữa x và y trong hàm số.
Bài 2: Vẽ đồ thị hàm số y = -x + 2.
Giải:
Trang 102 thường chứa các bài tập ứng dụng hàm số vào giải quyết các bài toán thực tế, ví dụ như bài toán về quãng đường, thời gian, vận tốc. Các bài tập này giúp học sinh thấy được tính ứng dụng của toán học trong cuộc sống.
Bài 3: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết công thức tính quãng đường đi được của ô tô theo thời gian đi.
Giải:
Gọi s là quãng đường đi được của ô tô (km), t là thời gian đi (giờ). Ta có công thức: s = 60t.
Để giải tốt các bài tập về hàm số bậc nhất, học sinh cần nắm vững các kiến thức sau:
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 2 trang 100, 101, 102 SGK Toán 9 tập 1. Chúc các em học tập tốt!