Chào mừng các em học sinh đến với bài giải bài tập 4.9 trang 86 SGK Toán 9 tập 1 của giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
Đề bài
Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
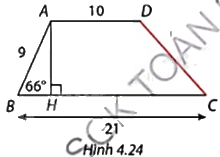
Phương pháp giải - Xem chi tiết
+ Kẻ DK vuông góc với BC tại K.
+ Tam giác AHB vuông tại H nên \(AH = AB.\sin B\).
+ Chứng minh tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH\).
+ Áp dụng định lí Pythagore vào tam giác DKC vuông tại K để tính CD.
Lời giải chi tiết
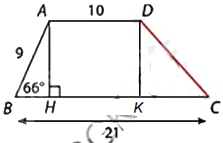
Kẻ DK vuông góc với BC tại K.
\(\Delta \)AHB vuông tại H nên
\(AH = AB.\sin B = 9.\sin {66^o} \approx 8,2\)
\(BH = AB.\cos B = 9.\cos {66^o} \approx 3,7\)
Tứ giác AHKD có: AD//HK (gt), AH//DK (cùng vuông góc với BC) nên tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH \approx 8,2\).
Độ dài đoạn thẳng KC là:
\(KC = BC - BH - HK \approx 21 - 3,7 - 10 = 7,3\)
\(\Delta \)DKC vuông tại K nên
\(D{C^2} = D{K^2} + K{C^2} \approx 8,{2^2} + {7,3^2} = 120,53\) (Định lí Pythagore) nên \(DC \approx 11\).
Bài tập 4.9 trang 86 SGK Toán 9 tập 1 yêu cầu chúng ta xét hàm số y = (m-2)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m - 2 ≠ 0. Bài viết này sẽ đi sâu vào phân tích điều kiện này và cách xác định giá trị của m để đảm bảo hàm số thỏa mãn yêu cầu.
Hàm số y = ax + b được gọi là hàm số bậc nhất khi và chỉ khi a ≠ 0. Trong trường hợp của bài tập này, a = m - 2. Do đó, để y = (m-2)x + 3 là hàm số bậc nhất, chúng ta cần có:
m - 2 ≠ 0
Giải bất phương trình này, ta được:
m ≠ 2
Khi m = 2, hàm số trở thành y = (2-2)x + 3 = 0x + 3 = 3. Đây là một hàm số hằng, không phải là hàm số bậc nhất. Do đó, việc loại trừ giá trị m = 2 là rất quan trọng để đảm bảo tính chất bậc nhất của hàm số.
Xét các trường hợp sau:
Hàm số trở thành y = (3-2)x + 3 = x + 3. Đây là hàm số bậc nhất với hệ số góc là 1.
Hàm số trở thành y = (0-2)x + 3 = -2x + 3. Đây là hàm số bậc nhất với hệ số góc là -2.
Hàm số trở thành y = (2-2)x + 3 = 3. Đây là hàm số hằng, không phải hàm số bậc nhất.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài tập 4.9 trang 86 SGK Toán 9 tập 1 là một bài tập cơ bản nhưng quan trọng để hiểu rõ điều kiện của hàm số bậc nhất. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài tập phức tạp hơn trong chương trình học.
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 4.9 trang 86 SGK Toán 9 tập 1. Chúc các em học tập tốt!