Chào mừng các em học sinh đến với bài giải bài tập 6.22 trang 22 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
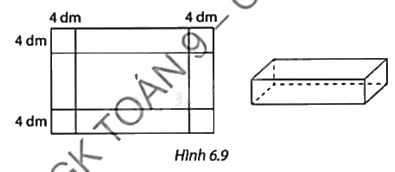
Từ một miếng tôn hình chữ nhật, người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 4 dm để tạo thành một cái thùng hình hộp chữ nhật không nắp có dung tích bằng 1536 dm3 (Hình 6.9). Tính kích thước của miếng tôn ban đầu, biết chiều dài của nó gấp đôi chiều rộng.
Đề bài
Từ một miếng tôn hình chữ nhật, người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 4 dm để tạo thành một cái thùng hình hộp chữ nhật không nắp có dung tích bằng 1536 dm3 (Hình 6.9). Tính kích thước của miếng tôn ban đầu, biết chiều dài của nó gấp đôi chiều rộng.
Phương pháp giải - Xem chi tiết
Bước 1: Lập phương trình:
Chọn ẩn số và đặt điều kiện cho ẩn số.
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Kiểm tra xem nghiệm có thoả mãn điều kiện của ẩn hay không rồi kết luận.
Lời giải chi tiết
Gọi chiều rộng của miếng tôn là x (dm), x > 5. Chiều dài của nó là 2x (dm).
Khi làm thành một cái thùng không đáy thì chiều dài của thùng là 2x - 5 (dm), chiều rộng là x - 5 (dm), chiều cao là 5 (dm).
Dung tích của thùng là 5.(2x-10).(x-10) (dm3)
Theo đầu bài ta có phương trình:
\({x^2} - 15x - 100 = 0\)
Giải phương trình ta được: \({x_1} = 20(TM);{x_2} = - 5(L)\)
Vậy miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40(dm).
Bài tập 6.22 trang 22 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Cụ thể, bài toán thường liên quan đến việc xác định phương trình đường thẳng tiếp xúc với đồ thị hàm số tại một điểm cho trước.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Thông thường, bài toán 6.22 sẽ cung cấp một hàm số bậc nhất và một điểm. Yêu cầu là tìm phương trình đường thẳng đi qua điểm đó và tiếp xúc với đồ thị hàm số đã cho.
Để giải bài toán này, chúng ta có thể thực hiện các bước sau:
Bài toán: Cho hàm số y = 2x + 1. Tìm phương trình đường thẳng đi qua điểm A(1; 3) và tiếp xúc với đồ thị hàm số.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về phương pháp tiếp tuyến, các em có thể luyện tập thêm các bài tập tương tự trong SGK Toán 9 tập 2 và các tài liệu tham khảo khác.
Hy vọng với bài giải chi tiết và những lưu ý trên, các em sẽ tự tin giải quyết bài tập 6.22 trang 22 SGK Toán 9 tập 2 một cách hiệu quả. Chúc các em học tốt!