Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1

Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 - Cùng khám phá

Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1

Bài tập 5.43 trang 129 SGK Toán 9 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai và ứng dụng vào các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và các phương pháp giải khác nhau để giúp bạn hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.

Từ điểm M vẽ tiếp tuyến MA đến đường tròn (O; 6cm) (A là tiếp điểm). Nếu \(MO = 10cm\) thì độ dài MA bằng A. 6cm. B. 7cm. C. 8cm. D. 9cm.

Đề bài

Từ điểm M vẽ tiếp tuyến MA đến đường tròn (O; 6cm) (A là tiếp điểm). Nếu \(MO = 10cm\) thì độ dài MA bằng

A. 6cm.

B. 7cm.

C. 8cm.

D. 9cm.

Phương pháp giải - Xem chi tiết Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 - Cùng khám phá 1

+ Chứng minh tam giác MAO vuông tại A.

+ Áp dụng định lí Pythagore vào tam giác MAO vuông tại A ta tính được MA.

Lời giải chi tiết

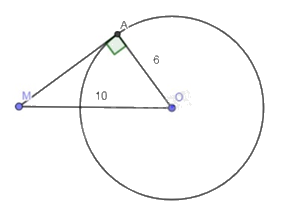
Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 - Cùng khám phá 2

Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác MAO vuông tại A.

Suy ra: \(M{A^2} + A{O^2} = M{O^2}\) (định lí Pythagore),

\(MA = \sqrt {M{O^2} - A{O^2}} = \sqrt {{{10}^2} - {6^2}} = 8\left( {cm} \right)\)

Chọn C

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 - Cùng khám phá đặc sắc thuộc chuyên mục giải sgk toán 9 trên nền tảng toán học. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1: Hướng dẫn chi tiết

Bài tập 5.43 trang 129 SGK Toán 9 tập 1 yêu cầu giải phương trình bậc hai. Để giải bài toán này, chúng ta cần nắm vững các kiến thức về phương trình bậc hai, bao gồm công thức nghiệm, điều kiện có nghiệm, và các phương pháp giải khác nhau.

1. Đề bài bài tập 5.43 trang 129 SGK Toán 9 tập 1

Đề bài thường có dạng: Giải phương trình (với phương trình cụ thể được đưa ra). Ví dụ, một đề bài có thể là: Giải phương trình 2x² - 5x + 2 = 0.

2. Phương pháp giải phương trình bậc hai

Có nhiều phương pháp để giải phương trình bậc hai, bao gồm:

Phương pháp phân tích thành nhân tử: Phương pháp này áp dụng khi phương trình có thể phân tích thành nhân tử một cách dễ dàng.
Phương pháp sử dụng công thức nghiệm: Đây là phương pháp tổng quát nhất, áp dụng cho mọi phương trình bậc hai. Công thức nghiệm của phương trình ax² + bx + c = 0 là:
x_1,2 = (-b ± √(b² - 4ac)) / 2a
Phương pháp hoàn thiện bình phương: Phương pháp này giúp biến đổi phương trình về dạng (x + m)² = n, từ đó dễ dàng tìm ra nghiệm.

3. Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 (Ví dụ)

Ví dụ: Giải phương trình 2x² - 5x + 2 = 0

Lời giải:

Xác định các hệ số: a = 2, b = -5, c = 2
Tính delta: Δ = b² - 4ac = (-5)² - 4 * 2 * 2 = 25 - 16 = 9
Tìm nghiệm: Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x₁ = (-(-5) + √9) / (2 * 2) = (5 + 3) / 4 = 2
x₂ = (-(-5) - √9) / (2 * 2) = (5 - 3) / 4 = 1/2
Kết luận: Phương trình có hai nghiệm là x₁ = 2 và x₂ = 1/2

4. Lưu ý khi giải phương trình bậc hai

Kiểm tra delta: Δ > 0: Phương trình có hai nghiệm phân biệt.
Δ = 0: Phương trình có nghiệm kép.
Δ < 0: Phương trình vô nghiệm.
Kiểm tra lại nghiệm: Sau khi tìm được nghiệm, cần kiểm tra lại bằng cách thay nghiệm vào phương trình ban đầu để đảm bảo tính chính xác.

5. Các bài tập tương tự

Để rèn luyện kỹ năng giải phương trình bậc hai, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 9 tập 1 và các tài liệu tham khảo khác.

6. Ứng dụng của phương trình bậc hai

Phương trình bậc hai có nhiều ứng dụng trong thực tế, chẳng hạn như:

Tính toán quỹ đạo của vật thể: Trong vật lý, phương trình bậc hai được sử dụng để tính toán quỹ đạo của vật thể ném lên không trung.
Thiết kế các công trình xây dựng: Trong kỹ thuật, phương trình bậc hai được sử dụng để thiết kế các công trình xây dựng như cầu, đường hầm.
Giải các bài toán kinh tế: Trong kinh tế, phương trình bậc hai được sử dụng để giải các bài toán về lợi nhuận, chi phí.

Hy vọng với hướng dẫn chi tiết này, bạn sẽ hiểu rõ hơn về cách giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 và tự tin giải các bài tập tương tự. Chúc bạn học tốt!