Chào mừng các em học sinh đến với bài giải bài tập 5.30 trang 126 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK, bài tập nâng cao và các tài liệu học tập hữu ích khác.
Tính các số đo x và y trong mỗi trường hợp ở Hình 5.69.
Đề bài
Tính các số đo x và y trong mỗi trường hợp ở Hình 5.69.
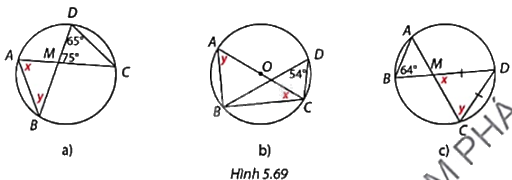
Phương pháp giải - Xem chi tiết
a) + Tam giác MDC có: \(\widehat {BDC} + \widehat {DCM} + \widehat {DMC} = {180^o}\), tính góc BDC.
+ Vì góc CAB và góc BDC là góc ở nội tiếp cùng chắn cung BC nên \(x = \widehat {BDC}\).
+ Vì góc ACD và góc ABD là góc ở nội tiếp cùng chắn cung AD nên \(y = \widehat {ACD}\).
b) + Vì góc BAC và góc BDC là góc ở nội tiếp cùng chắn cung nhỏ BC nên \(y = \widehat {BDC}\) và số đo cung BC nhỏ, từ đó tính số đo cung AB nhỏ.
+ Vì góc ACB là góc ở nội tiếp chắn cung nhỏ AB nên tính được góc ACB.
c) + Vì góc DBA và góc DCA là góc ở nội tiếp cùng chắn cung nhỏ AD nên \(y = \widehat {DCA}\).
+ Chứng minh \(\Delta \)MCD cân tại D. Do đó, \(x = y\)
Lời giải chi tiết
a) \(\Delta \)MDC có: \(\widehat {BDC} + \widehat {DCM} + \widehat {DMC} = {180^o}\) nên
\(\widehat {DCM} = {180^o} - \widehat D - \widehat {DMC} = {180^o} - {65^o} - {75^o} = {40^o}\)
Vì góc CAB và góc BDC là góc ở nội tiếp cùng chắn cung BC nên \(x = \widehat {BDC} = {65^o}\).
Vì góc ACD và góc ABD là góc ở nội tiếp cùng chắn cung AD nên \(y = \widehat {ACD} = {40^o}\).
b) Vì góc BAC và góc BDC là góc ở nội tiếp cùng chắn cung BC nên \(y = \widehat {BDC} = {54^o}\) và số đo cung BC nhỏ là: \({2.54^o} = {108^o}\).
Số đo cung AB nhỏ là: \({180^o} - {108^o} = {72^o}\).
Vì góc ACB là góc ở nội tiếp chắn cung nhỏ AB nên \(x = \frac{1}{2}{.72^o} = {36^o}\).
c) Vì góc DBA và góc DCA là góc ở nội tiếp cùng chắn cung AD nên \(y = \widehat {ABD} = {64^o}\).
Tam giác MCD có: \(MD = CD\) nên tam giác MCD cân tại D. Do đó, \(x = y = {64^o}\).
Bài tập 5.30 trang 126 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất và ứng dụng. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, cách xác định hệ số góc và tung độ gốc, cũng như các ứng dụng của hàm số bậc nhất trong thực tế.
Đề bài thường yêu cầu xác định hàm số bậc nhất đi qua hai điểm cho trước, hoặc tìm điều kiện để ba điểm thẳng hàng. Ngoài ra, bài tập có thể yêu cầu giải các bài toán thực tế liên quan đến hàm số bậc nhất, ví dụ như tính quãng đường đi được của một vật chuyển động đều, hoặc tính tiền lương của một công nhân theo thời gian làm việc.
Ví dụ: Cho hai điểm A(1, 2) và B(-1, 0). Hãy tìm hàm số bậc nhất y = ax + b đi qua hai điểm này.
Giải:
Ngoài bài tập 5.30, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và cách giải:
Để củng cố kiến thức và kỹ năng giải bài tập hàm số bậc nhất, các em có thể tự giải thêm các bài tập sau:
Bài tập 5.30 trang 126 SGK Toán 9 tập 1 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và lời giải trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Hệ số góc | Số a trong phương trình y = ax + b, thể hiện độ dốc của đường thẳng. |
| Tung độ gốc | Số b trong phương trình y = ax + b, là giá trị của y khi x = 0. |