Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 81, 82 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài học này tập trung vào việc... (nội dung giới thiệu ngắn gọn về chủ đề bài học)
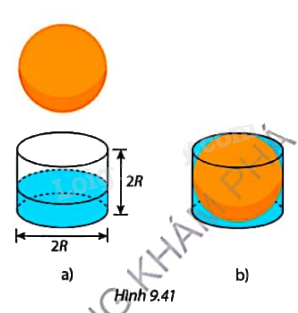
Bạn Mai thả từ từ một quả cầu bán kính R vào một chiếc cốc thuỷ tinh hình trụ chứa sẵn nước đến \(\frac{1}{3}\) chiều cao cốc (Hình 9.41a) thì thấy nước dâng lên vừa miệng cốc (Hình 9.41b). Dựa vào kết quả thí nghiệm của bạn Mai, viết công thức tính: a) Thể tích của chiếc cốc hình trụ theo R b) Thể tích của quả cầu.
Trả lời câu hỏi Vận dụng 3 trang 82SGK Toán 9 Cùng khám phá
Hãy trả lời câu hỏi ở phần Khởi động.
Phần Khởi động: Bán kính Sao Mộc gấp khoảng 11 lần bán kính Trái Đất. Vậy thể tích Sao Mộc gấp bao nhiêu lần thể tích Trái Đất?
Phương pháp giải:
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết:
Giả sử bán kính Trái Đất là R (R > 0) thì bán kính Sao Mộc là: 11R.
Thể tích Trái Đất là:
VTrái Đất = \(\frac{4}{3}\pi {R^3}\)
Thể tích Sao Mộc là:
VSao Mộc = \(\frac{4}{3}\pi {\left( {11R} \right)^3} = \frac{4}{3}\pi .1331{R^3}\)
Thể tích của Sao Mộc gấp thể tích Trái Đất là:
\(\frac{{\frac{4}{3}\pi .1331{R^3}}}{{\frac{4}{3}\pi .{R^3}}} = 1331\) (lần)
Vậy thể tích của Sao Mộc gấp 1331 lần thể tích Trái Đất.
Trả lời câu hỏi Luyện tập 3 trang 81SGK Toán 9 Cùng khám phá
Tính bán kính của một quả địa cầu có thể tích 14130 cm3, lấy \(\pi \approx 3,14\).

Phương pháp giải:
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết:
Ta có \(V = \frac{4}{3}\pi {R^3} = 14130\)
Suy ra R = \(\sqrt[3]{{\frac{{14130}}{{\frac{4}{3}.3,14}}}} = 15\)cm.
Trả lời câu hỏi Hoạt động 4 trang 81 SGK Toán 9 Cùng khám phá
Bạn Mai thả từ từ một quả cầu bán kính R vào một chiếc cốc thuỷ tinh hình trụ chứa sẵn nước đến \(\frac{1}{3}\) chiều cao cốc (Hình 9.41a) thì thấy nước dâng lên vừa miệng cốc (Hình 9.41b). Dựa vào kết quả thí nghiệm của bạn Mai, viết công thức tính:
a) Thể tích của chiếc cốc hình trụ theo R
b) Thể tích của quả cầu.
Phương pháp giải:
Thể tích hình trụ là: \(V = \pi {R^2}h\).
Từ đó suy ra thể tích của quả cầu.
Lời giải chi tiết:
a) Thể tích hình trụ là:
\(V = \pi .{R^2}.2R = 2\pi {R^3}\).
b) Thể tích của quả cầu là:
\(V = \frac{2}{3}.2\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Trả lời câu hỏi Vận dụng 4 trang 82SGK Toán 9 Cùng khám phá
Tính diện tích bề mặt ngoài và thể tích của một ống nghiệm có phần thân hình trụ và đáy là nửa hình cầu với kích thước như Hình 9.43.
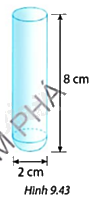
Phương pháp giải:
Diện tích xung quanh hình trụ là:
\(S = 2\pi Rh\)
Thể tích của hình trụ là:
\(V = \pi {R^2}h\)
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)
Thể tích của hình cầu là:
\(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết:
Diện tích mặt ngoài của phần hình trụ cao 8cm là:
\(S = 2\pi Rh = 2\pi .1.8 = 16\pi \) (cm2)
Diện tích nửa mặt cầu là:
\(S = 2\pi {R^2} = 2\pi {.1^2} = 2\pi \) (cm2)
Diện tích phần hình trụ ống nghiệm là:
\(16\pi - 2\pi = 14\pi \)(cm2)
Vậy diện tích mặt ngoài ống nghiệm là:
\(14\pi + 2\pi = 16\pi \) (cm2)
Thể tích hình trụ cao 8 cm là:
\(V = \pi {R^2}h = \pi .1{}^2.8 = 8\pi \) (cm3)
Thể tích nửa hình cầu:
\(V = \frac{2}{3}\pi {.1^3} = \frac{2}{3}\pi \) (cm3)
Thể tích phần hình trụ ống nghiệm là:
\(8\pi - \frac{2}{3}\pi = \frac{{22}}{3}\pi \) (cm3)
Thể tích của ống nghiệm là:
\(\frac{{22}}{3}\pi + \frac{2}{3}\pi = 8\pi \) (cm3)
Trả lời câu hỏi Hoạt động 4 trang 81 SGK Toán 9 Cùng khám phá
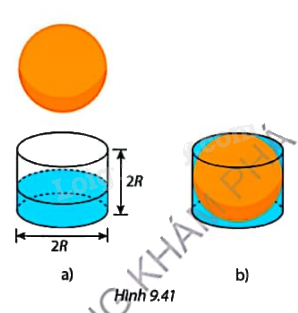
Bạn Mai thả từ từ một quả cầu bán kính R vào một chiếc cốc thuỷ tinh hình trụ chứa sẵn nước đến \(\frac{1}{3}\) chiều cao cốc (Hình 9.41a) thì thấy nước dâng lên vừa miệng cốc (Hình 9.41b). Dựa vào kết quả thí nghiệm của bạn Mai, viết công thức tính:
a) Thể tích của chiếc cốc hình trụ theo R
b) Thể tích của quả cầu.
Phương pháp giải:
Thể tích hình trụ là: \(V = \pi {R^2}h\).
Từ đó suy ra thể tích của quả cầu.
Lời giải chi tiết:
a) Thể tích hình trụ là:
\(V = \pi .{R^2}.2R = 2\pi {R^3}\).
b) Thể tích của quả cầu là:
\(V = \frac{2}{3}.2\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Trả lời câu hỏi Luyện tập 3 trang 81SGK Toán 9 Cùng khám phá
Tính bán kính của một quả địa cầu có thể tích 14130 cm3, lấy \(\pi \approx 3,14\).

Phương pháp giải:
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết:
Ta có \(V = \frac{4}{3}\pi {R^3} = 14130\)
Suy ra R = \(\sqrt[3]{{\frac{{14130}}{{\frac{4}{3}.3,14}}}} = 15\)cm.
Trả lời câu hỏi Vận dụng 3 trang 82SGK Toán 9 Cùng khám phá
Hãy trả lời câu hỏi ở phần Khởi động.
Phần Khởi động: Bán kính Sao Mộc gấp khoảng 11 lần bán kính Trái Đất. Vậy thể tích Sao Mộc gấp bao nhiêu lần thể tích Trái Đất?
Phương pháp giải:
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết:
Giả sử bán kính Trái Đất là R (R > 0) thì bán kính Sao Mộc là: 11R.
Thể tích Trái Đất là:
VTrái Đất = \(\frac{4}{3}\pi {R^3}\)
Thể tích Sao Mộc là:
VSao Mộc = \(\frac{4}{3}\pi {\left( {11R} \right)^3} = \frac{4}{3}\pi .1331{R^3}\)
Thể tích của Sao Mộc gấp thể tích Trái Đất là:
\(\frac{{\frac{4}{3}\pi .1331{R^3}}}{{\frac{4}{3}\pi .{R^3}}} = 1331\) (lần)
Vậy thể tích của Sao Mộc gấp 1331 lần thể tích Trái Đất.
Trả lời câu hỏi Vận dụng 4 trang 82SGK Toán 9 Cùng khám phá
Tính diện tích bề mặt ngoài và thể tích của một ống nghiệm có phần thân hình trụ và đáy là nửa hình cầu với kích thước như Hình 9.43.
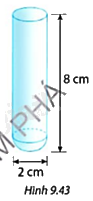
Phương pháp giải:
Diện tích xung quanh hình trụ là:
\(S = 2\pi Rh\)
Thể tích của hình trụ là:
\(V = \pi {R^2}h\)
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)
Thể tích của hình cầu là:
\(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết:
Diện tích mặt ngoài của phần hình trụ cao 8cm là:
\(S = 2\pi Rh = 2\pi .1.8 = 16\pi \) (cm2)
Diện tích nửa mặt cầu là:
\(S = 2\pi {R^2} = 2\pi {.1^2} = 2\pi \) (cm2)
Diện tích phần hình trụ ống nghiệm là:
\(16\pi - 2\pi = 14\pi \)(cm2)
Vậy diện tích mặt ngoài ống nghiệm là:
\(14\pi + 2\pi = 16\pi \) (cm2)
Thể tích hình trụ cao 8 cm là:
\(V = \pi {R^2}h = \pi .1{}^2.8 = 8\pi \) (cm3)
Thể tích nửa hình cầu:
\(V = \frac{2}{3}\pi {.1^3} = \frac{2}{3}\pi \) (cm3)
Thể tích phần hình trụ ống nghiệm là:
\(8\pi - \frac{2}{3}\pi = \frac{{22}}{3}\pi \) (cm3)
Thể tích của ống nghiệm là:
\(\frac{{22}}{3}\pi + \frac{2}{3}\pi = 8\pi \) (cm3)
Mục 3 trang 81, 82 SGK Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Đây là một phần quan trọng, nền tảng cho các kiến thức nâng cao hơn trong chương trình học. Bài viết này sẽ cung cấp lời giải chi tiết từng bài tập, kèm theo phương pháp giải và các lưu ý quan trọng để giúp các em học sinh hiểu rõ hơn về chủ đề này.
Mục 3 bao gồm các bài tập vận dụng kiến thức về:
Đề bài: (Nội dung đề bài)
Lời giải: (Lời giải chi tiết bài tập 1, kèm theo giải thích từng bước)
Đề bài: (Nội dung đề bài)
Lời giải: (Lời giải chi tiết bài tập 2, kèm theo giải thích từng bước)
Đề bài: (Nội dung đề bài)
Lời giải: (Lời giải chi tiết bài tập 3, kèm theo giải thích từng bước)
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, các em cần lưu ý:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng với bài giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ hiểu rõ hơn về mục 3 trang 81, 82 SGK Toán 9 tập 2 và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!