Bài tập 5.29 trang 122 SGK Toán 9 tập 1 là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng thực tế để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
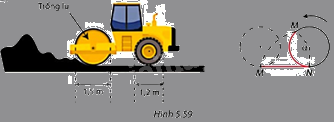
Một chiếc xe lu có đường kính trống lu là 1,5m và đường kính của bánh sau là 1,2m (Hình 5.59). Khi hoạt động, trống lu quay hết một vòng \(\left( {{{360}^o}} \right)\) trong 5 phút. a) Trong mỗi phút, trống lu quay được bao nhiêu độ và xe lu cán được bao nhiêu mét đường? b) Để cán được 1 mét đường thì trống lu phải quay một góc bao nhiêu độ? c) Để trống lu quay được 1 vòng thì bánh sau phải quay bao nhiêu vòng?
Đề bài
Một chiếc xe lu có đường kính trống lu là 1,5m và đường kính của bánh sau là 1,2m (Hình 5.59). Khi hoạt động, trống lu quay hết một vòng \(\left( {{{360}^o}} \right)\) trong 5 phút.
a) Trong mỗi phút, trống lu quay được bao nhiêu độ và xe lu cán được bao nhiêu mét đường?
b) Để cán được 1 mét đường thì trống lu phải quay một góc bao nhiêu độ?
c) Để trống lu quay được 1 vòng thì bánh sau phải quay bao nhiêu vòng?
Phương pháp giải - Xem chi tiết
a) Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
b) Công thức tính độ dài C của đường tròn bán kính R là: \(C = 2\pi R\)
Lời giải chi tiết
a) Bán kính trống lu là:
\(\frac{{1,5}}{2} = 0,75\left( m \right)\).
Trong một phút, trống lu quay được \(\frac{{{{360}^o}}}{5} = {72^o}\).
Trong một phút, lu xe cán được số mét đường là:
\(l = \frac{{\pi .0,75.72}}{{180}} = \frac{{3\pi }}{{10}}\left( m \right)\).
b) Trống lu cán được 1m đường thì ta có:
\(1 = \frac{{\pi .0,75n}}{{180}}\), suy ra: \(n = \frac{{240}}{\pi }\).
Vậy để cán được 1 mét đường thì trống lu phải quay thì trống lu phải quay một góc \(\frac{{240}}{\pi } \approx {76^o}\).
c) Độ dài đường tròn đường kính 1,5m là:
\({C_1} = 1,5\pi \left( {cm} \right)\).
Độ dài đường tròn đường kính 1,2m là:
\({C_2} = 1,2\pi \left( {cm} \right)\).
Ta có: \(\frac{{{C_1}}}{{{C_2}}} = \frac{{1,5\pi }}{{1,2\pi }} = 1,25\).
Vậy khi trống lu quay được 1 vòng thì bánh sau xe quay được 1,25 vòng.
Bài tập 5.29 trang 122 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài toán này thường gặp trong các bài kiểm tra và thi học kỳ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Đề bài: (SGK Toán 9 tập 1, trang 122)
(Giả sử đề bài là: Một người đi xe đạp từ A đến B với vận tốc 12km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 36km?)
Lời giải:
Gọi t (giờ) là thời gian người đó đi từ A đến B.
Quãng đường AB là 36km, vận tốc của người đi xe đạp là 12km/h. Ta có công thức:
Quãng đường = Vận tốc × Thời gian
=> 36 = 12 × t
=> t = 36 / 12 = 3 (giờ)
Vậy người đó đi hết 3 giờ để đi từ A đến B.
Phân tích bài toán:
Bài toán này là một ứng dụng thực tế của hàm số bậc nhất. Trong trường hợp này, quãng đường đi được là hàm số của thời gian, với vận tốc là hệ số góc. Việc hiểu rõ mối quan hệ giữa quãng đường, vận tốc và thời gian là chìa khóa để giải quyết bài toán này.
Các dạng bài tập tương tự:
Mẹo giải bài tập:
Ví dụ 1: (Tương tự bài tập 5.29)
Một ô tô đi từ thành phố A đến thành phố B với vận tốc 60km/h. Hỏi ô tô đó đi hết bao lâu nếu quãng đường AB dài 180km?
Lời giải:
Thời gian ô tô đi từ A đến B là: t = 180 / 60 = 3 (giờ)
Ví dụ 2: (Bài tập nâng cao)
Một người đi bộ từ A đến B với vận tốc 5km/h. Sau 1 giờ, người đó tăng vận tốc lên 7km/h. Hỏi người đó đi hết bao lâu để đến B, biết quãng đường AB dài 20km?
Lời giải:
Trong 1 giờ đầu, người đó đi được 5km. Quãng đường còn lại là 20 - 5 = 15km.
Thời gian người đó đi quãng đường còn lại với vận tốc 7km/h là: t = 15 / 7 ≈ 2.14 (giờ)
Tổng thời gian người đó đi từ A đến B là: 1 + 2.14 = 3.14 (giờ)
Kết luận:
Việc nắm vững kiến thức về hàm số bậc nhất và các ứng dụng thực tế là rất quan trọng để giải quyết các bài tập toán học. Hãy luyện tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc các nguồn tài liệu học tập uy tín để đạt kết quả tốt nhất.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải bài tập 5.29 trang 122 SGK Toán 9 tập 1 và các bài tập tương tự.