Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 2, 3 SGK Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Viết hàm số biểu thị diện tích S (cm2) của tam giác vuông cân có độ dài cạnh góc vuông bằng x (cm). Tính S khi x lần lượt bằng 2 cm, 2,5 cm, 6 cm.
Trả lời câu hỏi Vận dụng 1 trang 3 SGK Toán 9 Cùng khám phá
Một vật rơi ở độ cao 80 m sao với mặt đất. Quãng đường chuyển động s (m) của vật rơi phụ thuộc vào thời gian t (s) bởi công thức s = 5t2.
a) Tính quãng đường chuyển động của vật sau 2 giây.
b) Hỏi sau bao lâu vật này tiếp đất?
Phương pháp giải:
Thay t = 2 vào s = 5t2 để tìm s.
Thay s = 80 vào s = 5t2 để tìm t (t > 0).
Lời giải chi tiết:
a) Quãng đường chuyển động của vật sau 2 giây là:
s = 5.22 = 20 (m)
b) Để vật tiếp đất thì quãng đường vật đi được là 80 m thay vào s = 5t2 (t > 0) ta có:
\(\begin{array}{l}5{t^2} = 80\\{t^2} = 16\\\left[ {\begin{array}{*{20}{c}}{t = 4(TM)}\\{t = - 4(L)}\end{array}} \right.\end{array}\)
Vậy sau 4 giây thì vật tiếp đất.
Trả lời câu hỏi Hoạt động 1 trang 2SGK Toán 9 Cùng khám phá
Viết hàm số biểu thị diện tích S (cm2) của tam giác vuông cân có độ dài cạnh góc vuông bằng x (cm). Tính S khi x lần lượt bằng 2 cm, 2,5 cm, 6 cm.
Phương pháp giải:
Dựa vào công thức diện tích tam giác vuông cân: S = \(\frac{1}{2}{x^2}\) (x là độ dài cạnh góc vuông).
Thay lần lượt x = 2; x = 2,5; x = 6 để tính S.
Lời giải chi tiết:
Ta có hàm số biểu thị diện tích S = \(\frac{1}{2}{x^2}\)
Với x = 2 ta có S = \(\frac{1}{2}{.2^2} = 2\)cm2
Với x = 2,5 ta có S = \(\frac{1}{2}.2,{5^2} = \frac{{25}}{8}\)cm2
Với x = 6 ta có S = \(\frac{1}{2}{.6^2} = 18\)cm2
Trả lời câu hỏi Luyện tập 1 trang 2 SGK Toán 9 Cùng khám phá
Cho hàm số \(y = a{x^2}\).
a) Tìm a khi biết x = 2 thì y = - 1.
b) Tính các giá trị tương ứng của hàm số trong bảng 6.1
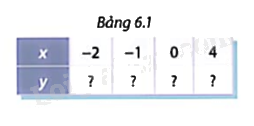
Phương pháp giải:
Thay x = 2; y = -1 vào \(y = a{x^2}\) để tìm a.
Thay lần lượt x = -2; x = -1; x = 0; x = 4 để tìm y.
Lời giải chi tiết:
a) Thay x = 2; y = -1 vào \(y = a{x^2}\) ta có:
\(\begin{array}{l} - 1 = a{.2^2}\\a = - \frac{1}{4}\end{array}\)
b) \(y = - \frac{1}{4}{x^2}\)
Với x = -2 thì \(y = - \frac{1}{4}{\left( { - 2} \right)^2} = - \frac{1}{4}.4 = - 1\)
Với x = -1 thì \(y = - \frac{1}{4}{\left( { - 1} \right)^2} = - \frac{1}{4}.1 = - \frac{1}{4}\)
Với x = 0 thì \(y = - \frac{1}{4}{.0^2} = 0\)
Với x = 4 thì \(y = - \frac{1}{4}{\left( 4 \right)^2} = - \frac{1}{4}.16 = - 4\)

Trả lời câu hỏi Hoạt động 1 trang 2SGK Toán 9 Cùng khám phá
Viết hàm số biểu thị diện tích S (cm2) của tam giác vuông cân có độ dài cạnh góc vuông bằng x (cm). Tính S khi x lần lượt bằng 2 cm, 2,5 cm, 6 cm.
Phương pháp giải:
Dựa vào công thức diện tích tam giác vuông cân: S = \(\frac{1}{2}{x^2}\) (x là độ dài cạnh góc vuông).
Thay lần lượt x = 2; x = 2,5; x = 6 để tính S.
Lời giải chi tiết:
Ta có hàm số biểu thị diện tích S = \(\frac{1}{2}{x^2}\)
Với x = 2 ta có S = \(\frac{1}{2}{.2^2} = 2\)cm2
Với x = 2,5 ta có S = \(\frac{1}{2}.2,{5^2} = \frac{{25}}{8}\)cm2
Với x = 6 ta có S = \(\frac{1}{2}{.6^2} = 18\)cm2
Trả lời câu hỏi Luyện tập 1 trang 2 SGK Toán 9 Cùng khám phá
Cho hàm số \(y = a{x^2}\).
a) Tìm a khi biết x = 2 thì y = - 1.
b) Tính các giá trị tương ứng của hàm số trong bảng 6.1
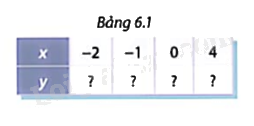
Phương pháp giải:
Thay x = 2; y = -1 vào \(y = a{x^2}\) để tìm a.
Thay lần lượt x = -2; x = -1; x = 0; x = 4 để tìm y.
Lời giải chi tiết:
a) Thay x = 2; y = -1 vào \(y = a{x^2}\) ta có:
\(\begin{array}{l} - 1 = a{.2^2}\\a = - \frac{1}{4}\end{array}\)
b) \(y = - \frac{1}{4}{x^2}\)
Với x = -2 thì \(y = - \frac{1}{4}{\left( { - 2} \right)^2} = - \frac{1}{4}.4 = - 1\)
Với x = -1 thì \(y = - \frac{1}{4}{\left( { - 1} \right)^2} = - \frac{1}{4}.1 = - \frac{1}{4}\)
Với x = 0 thì \(y = - \frac{1}{4}{.0^2} = 0\)
Với x = 4 thì \(y = - \frac{1}{4}{\left( 4 \right)^2} = - \frac{1}{4}.16 = - 4\)

Trả lời câu hỏi Vận dụng 1 trang 3 SGK Toán 9 Cùng khám phá
Một vật rơi ở độ cao 80 m sao với mặt đất. Quãng đường chuyển động s (m) của vật rơi phụ thuộc vào thời gian t (s) bởi công thức s = 5t2.
a) Tính quãng đường chuyển động của vật sau 2 giây.
b) Hỏi sau bao lâu vật này tiếp đất?
Phương pháp giải:
Thay t = 2 vào s = 5t2 để tìm s.
Thay s = 80 vào s = 5t2 để tìm t (t > 0).
Lời giải chi tiết:
a) Quãng đường chuyển động của vật sau 2 giây là:
s = 5.22 = 20 (m)
b) Để vật tiếp đất thì quãng đường vật đi được là 80 m thay vào s = 5t2 (t > 0) ta có:
\(\begin{array}{l}5{t^2} = 80\\{t^2} = 16\\\left[ {\begin{array}{*{20}{c}}{t = 4(TM)}\\{t = - 4(L)}\end{array}} \right.\end{array}\)
Vậy sau 4 giây thì vật tiếp đất.
Mục 1 của SGK Toán 9 tập 2 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong chương trình. Việc nắm vững các khái niệm, tính chất và phương pháp giải các bài toán liên quan đến hàm số bậc nhất là vô cùng cần thiết.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. Để hiểu rõ về hàm số bậc nhất, học sinh cần nắm vững các khái niệm sau:
Các bài tập trong mục 1 trang 2, 3 thường yêu cầu học sinh:
Bài 1: Cho hàm số y = 2x - 1. Hãy xác định hệ số góc và tung độ gốc của hàm số. Hàm số này đồng biến hay nghịch biến?
Giải:
Bài 2: Vẽ đồ thị của hàm số y = -x + 3.
Giải:
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, học sinh nên:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi đối mặt với các bài toán về hàm số bậc nhất trong SGK Toán 9 tập 2. Chúc các em học tập tốt!