Chào mừng các em học sinh đến với bài giải bài tập 9.3 trang 68 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng cung cấp các phương pháp giải khác nhau để các em có thể lựa chọn cách phù hợp nhất với bản thân.
Từ một tấm bìa hình chữ nhật với đồ dài hai cạnh là 20 cm, 15 cm có thể cuộn lại và dùng băng dính dán thành hình trụ A hoặc hình trụ B (không có nắp) như Hình 9.13. a) Hãy so sánh thể tích của hai hình trụ A và B. Giải thích câu trả lời của em. b) Nếu cắt tấm bìa thành hai phần X, Y bằng nhau và tạo thành hai hình trụ (không có nắp) cùng chiều cao 15 cm thì tổng thể tích của hai hình trụ này có lớn hơn thể tích của hình trụ B không? Vì sao?
Đề bài
Từ một tấm bìa hình chữ nhật với đồ dài hai cạnh là 20 cm, 15 cm có thể cuộn lại và dùng băng dính dán thành hình trụ A hoặc hình trụ B (không có nắp) như Hình 9.13.
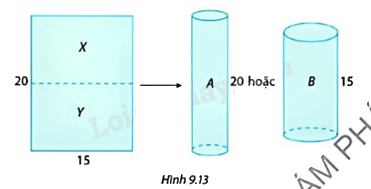
a) Hãy so sánh thể tích của hai hình trụ A và B. Giải thích câu trả lời của em.
b) Nếu cắt tấm bìa thành hai phần X, Y bằng nhau và tạo thành hai hình trụ (không có nắp) cùng chiều cao 15 cm thì tổng thể tích của hai hình trụ này có lớn hơn thể tích của hình trụ B không? Vì sao?
Phương pháp giải - Xem chi tiết
Dựa vào chu vi đường tròn C = \(2\pi r\) (với r là bán kính đường tròn).
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ).
Lời giải chi tiết
a) Ta có chu vi đường tròn đáy hình trụ A là:
\(2\pi r = 15\)suy ra r = \(\frac{{15}}{{2\pi }}\) cm
Thể tích hình trụ A là:
\({V_A} = \pi {r^2}h = \pi .{\left( {\frac{{15}}{{2\pi }}} \right)^2}.20 = \frac{{1125}}{\pi }\) cm3
Ta có chu vi đường tròn đáy hình trụ B là:
\(2\pi r = 20\)suy ra r = \(\frac{{20}}{{2\pi }} = \frac{{10}}{\pi }\) cm
Thể tích hình trụ B là:
\({V_B} = \pi {r^2}h = \pi .{\left( {\frac{{10}}{\pi }} \right)^2}.15 = \frac{{1500}}{\pi }\) cm3
Vậy thể tích hình trụ B lớn hơn thể tích hình trụ A.
b) Ta có chu vi đường tròn đáy hình trụ chiều cao 15 cm là:
\(2\pi r = 10\)suy ra r = \(\frac{5}{\pi }\) cm
Thể tích hình trụ chiều cao 15 cm là:
\(\pi {r^2}h = \pi .{\left( {\frac{5}{\pi }} \right)^2}.15 = \frac{{375}}{\pi }\) cm3
Suy ra thể tích hai hình trụ chiều cao 15 cm là:
2. \(\frac{{375}}{\pi }\) = \(\frac{{750}}{\pi }\) cm3
Vậy tổng thể tích của hai hình trụ chiều cao 15 cm nhỏ hơn thể tích của hình trụ B.
Bài tập 9.3 trang 68 SGK Toán 9 tập 2 yêu cầu chúng ta tìm hiểu và vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Sau đó, chúng ta cần lựa chọn phương pháp giải phù hợp. Đối với bài tập 9.3, phương pháp giải thường được sử dụng là:
Để minh họa phương pháp giải, chúng ta sẽ cùng nhau giải bài tập 9.3 trang 68 SGK Toán 9 tập 2. (Giả sử đề bài là: Tìm hàm số bậc nhất y = ax + b biết rằng đồ thị của hàm số đi qua hai điểm A(0; -2) và B(2; 0)).
Bước 1: Xác định hàm số
Hàm số cần tìm có dạng y = ax + b.
Bước 2: Tìm hệ số góc a và tung độ gốc b
Vì đồ thị của hàm số đi qua điểm A(0; -2), ta có: -2 = a * 0 + b => b = -2.
Vì đồ thị của hàm số đi qua điểm B(2; 0), ta có: 0 = a * 2 + b => 0 = 2a - 2 => a = 1.
Bước 3: Viết phương trình hàm số
Thay a = 1 và b = -2 vào dạng tổng quát, ta có phương trình hàm số: y = x - 2.
Ngoài bài tập 9.3, còn rất nhiều bài tập tương tự về hàm số bậc nhất. Các bài tập này thường yêu cầu chúng ta:
Để giải các bài tập này, chúng ta cần nắm vững các kiến thức và kỹ năng đã học, đồng thời luyện tập thường xuyên để nâng cao khả năng giải toán.
Khi giải bài tập về hàm số bậc nhất, chúng ta cần lưu ý một số điều sau:
Bài tập 9.3 trang 68 SGK Toán 9 tập 2 là một bài tập quan trọng giúp chúng ta hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số góc | a, xác định độ dốc của đường thẳng |
| Tung độ gốc | b, giao điểm của đường thẳng với trục Oy |