Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 4 trang 79, 80, 81 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Sử dụng máy tính cầm tay, hãy tính \(\cos {13^o}\) và \(\tan {71^o}25'\). Làm tròn kết quả đến hàng phần trăm.
Trả lời câu hỏi Luyện tập 6 trang 81 SGK Toán 9 Cùng khám phá
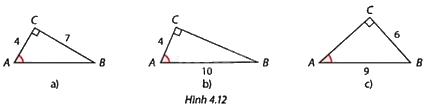
Xác định số đo góc nhọn A của tam giác vuông ABC trong mỗi trường hợp ở Hình 4.12. Làm tròn kết quả đến độ.
Phương pháp giải:
Hình a: Tính tanA, từ đó tính góc A.
Hình b: Tính cosA, từ đó tính góc A.
Hình c: Tính sinA, từ đó tính góc A.
Lời giải chi tiết:
Hình a: Tam giác ABC vuông tại C nên \(\tan A = \frac{{CB}}{{CA}} = \frac{7}{4}\) nên \(\widehat A \approx {60^o}\).
Hình b: Tam giác ABC vuông tại C nên \(\cos A = \frac{{CA}}{{AB}} = \frac{4}{{10}} = \frac{2}{5}\) nên \(\widehat A \approx {66^o}\).
Hình c: Tam giác ABC vuông tại C nên \(\sin A = \frac{{CB}}{{AB}} = \frac{6}{9} = \frac{2}{3}\) nên \(\widehat A \approx {42^o}\).
Trả lời câu hỏi Vận dụng trang 80 SGK Toán 9 Cùng khám phá
Độ dốc của ram dốc AB từ mặt đất xuống tầng hầm được tính bằng tỉ số của chiều sâu AH và chiều dài BH của phần đường hầm dành để xây dựng ram dốc (Hình 4.11). Theo quy chuẩn kĩ thuật quốc gia về công trình ngầm đô thị (QCVN 08:2009/BXD, phần 2- về gara ô tô), ram dốc thẳng cần có độ dốc không lớn hơn 18%. Em hãy cho biết ram dốc trong Hình 4.11 có đạt chuẩn về độ dốc không, nếu góc nghiêng ABH của ram dốc so với phương ngang là:
a) \({15^o}\);
b) \({9^o}\).

Phương pháp giải:
Tam giác ABH vuông tại H nên \(\tan B = \frac{{AH}}{{BH}}\).
Lời giải chi tiết:
Tam giác ABH vuông tại H nên \(\frac{{AH}}{{BH}} = \tan ABH\).
a) Với \(\widehat {ABH} = {15^o}\) thì độ dốc là: \(\tan {15^o} = 2 - \sqrt 3 > 18\% \) nên ram dốc không đạt tiêu chuẩn về độ dốc.
b) Với \(\widehat {ABH} = {9^o}\) thì độ dốc là: \(AB = \tan {9^o} \approx 0,158 < 18\% \) nên ram dốc đạt tiêu chuẩn về độ dốc.
Trả lời câu hỏi Luyện tập 4 trang 79 SGK Toán 9 Cùng khám phá
Sử dụng máy tính cầm tay, hãy tính \(\cos {13^o}\) và \(\tan {71^o}25'\). Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Sử dụng máy tính cầm tay để tính.
Lời giải chi tiết:
Để tính \(\cos {13^o}\), ta lần lượt bấm các nút

Ta được kết quả:

Do đó, \(\cos {13^o} \approx 0,97\)
Để tính \(\tan {71^o}25'\), ta lần lượt bấm các nút

Ta được kết quả:
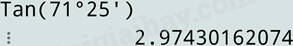
Do đó, \(\tan {71^o}25' \approx 2,97\).
Trả lời câu hỏi Luyện tập 5 trang 81 SGK Toán 9 Cùng khám phá
Sử dụng máy tính cầm tay, hãy tìm góc nhọn \(\alpha \), biết:
a) \(\cos \alpha = 0,8\);
b) \(\tan \alpha = 5\).
Làm tròn kết quả đến giây.
Phương pháp giải:
Sử dụng máy tính cầm tay để tìm góc nhọn.
Lời giải chi tiết:
a) Để tính góc \(\alpha \) có \(\cos \alpha = 0,8\), ta lần lượt bấm các nút

và được kết quả

Vậy \(\alpha \approx {36^o}52'12''\).
b) Để tính góc \(\alpha \) có \(\tan \alpha = 5\), ta lần lượt bấm các nút

và được kết quả

Vậy \(\alpha \approx {78^o}41'24''\).
Trả lời câu hỏi Luyện tập 4 trang 79 SGK Toán 9 Cùng khám phá
Sử dụng máy tính cầm tay, hãy tính \(\cos {13^o}\) và \(\tan {71^o}25'\). Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Sử dụng máy tính cầm tay để tính.
Lời giải chi tiết:
Để tính \(\cos {13^o}\), ta lần lượt bấm các nút

Ta được kết quả:

Do đó, \(\cos {13^o} \approx 0,97\)
Để tính \(\tan {71^o}25'\), ta lần lượt bấm các nút

Ta được kết quả:
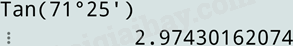
Do đó, \(\tan {71^o}25' \approx 2,97\).
Trả lời câu hỏi Vận dụng trang 80 SGK Toán 9 Cùng khám phá
Độ dốc của ram dốc AB từ mặt đất xuống tầng hầm được tính bằng tỉ số của chiều sâu AH và chiều dài BH của phần đường hầm dành để xây dựng ram dốc (Hình 4.11). Theo quy chuẩn kĩ thuật quốc gia về công trình ngầm đô thị (QCVN 08:2009/BXD, phần 2- về gara ô tô), ram dốc thẳng cần có độ dốc không lớn hơn 18%. Em hãy cho biết ram dốc trong Hình 4.11 có đạt chuẩn về độ dốc không, nếu góc nghiêng ABH của ram dốc so với phương ngang là:
a) \({15^o}\);
b) \({9^o}\).

Phương pháp giải:
Tam giác ABH vuông tại H nên \(\tan B = \frac{{AH}}{{BH}}\).
Lời giải chi tiết:
Tam giác ABH vuông tại H nên \(\frac{{AH}}{{BH}} = \tan ABH\).
a) Với \(\widehat {ABH} = {15^o}\) thì độ dốc là: \(\tan {15^o} = 2 - \sqrt 3 > 18\% \) nên ram dốc không đạt tiêu chuẩn về độ dốc.
b) Với \(\widehat {ABH} = {9^o}\) thì độ dốc là: \(AB = \tan {9^o} \approx 0,158 < 18\% \) nên ram dốc đạt tiêu chuẩn về độ dốc.
Trả lời câu hỏi Luyện tập 5 trang 81 SGK Toán 9 Cùng khám phá
Sử dụng máy tính cầm tay, hãy tìm góc nhọn \(\alpha \), biết:
a) \(\cos \alpha = 0,8\);
b) \(\tan \alpha = 5\).
Làm tròn kết quả đến giây.
Phương pháp giải:
Sử dụng máy tính cầm tay để tìm góc nhọn.
Lời giải chi tiết:
a) Để tính góc \(\alpha \) có \(\cos \alpha = 0,8\), ta lần lượt bấm các nút

và được kết quả

Vậy \(\alpha \approx {36^o}52'12''\).
b) Để tính góc \(\alpha \) có \(\tan \alpha = 5\), ta lần lượt bấm các nút

và được kết quả

Vậy \(\alpha \approx {78^o}41'24''\).
Trả lời câu hỏi Luyện tập 6 trang 81 SGK Toán 9 Cùng khám phá
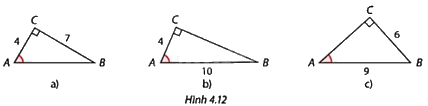
Xác định số đo góc nhọn A của tam giác vuông ABC trong mỗi trường hợp ở Hình 4.12. Làm tròn kết quả đến độ.
Phương pháp giải:
Hình a: Tính tanA, từ đó tính góc A.
Hình b: Tính cosA, từ đó tính góc A.
Hình c: Tính sinA, từ đó tính góc A.
Lời giải chi tiết:
Hình a: Tam giác ABC vuông tại C nên \(\tan A = \frac{{CB}}{{CA}} = \frac{7}{4}\) nên \(\widehat A \approx {60^o}\).
Hình b: Tam giác ABC vuông tại C nên \(\cos A = \frac{{CA}}{{AB}} = \frac{4}{{10}} = \frac{2}{5}\) nên \(\widehat A \approx {66^o}\).
Hình c: Tam giác ABC vuông tại C nên \(\sin A = \frac{{CB}}{{AB}} = \frac{6}{9} = \frac{2}{3}\) nên \(\widehat A \approx {42^o}\).
Mục 4 của SGK Toán 9 tập 1 thường tập trung vào các chủ đề như hàm số bậc nhất, đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các kiến thức tiếp theo trong chương trình Toán 9.
Bài tập này thường yêu cầu học sinh xác định hệ số góc và tung độ gốc của hàm số bậc nhất. Để giải bài tập này, các em cần nắm vững định nghĩa của hàm số bậc nhất và cách xác định các hệ số tương ứng.
Ví dụ: Cho hàm số y = 2x + 3. Xác định hệ số góc và tung độ gốc của hàm số.
Lời giải: Hệ số góc là 2, tung độ gốc là 3.
Bài tập này thường yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị, các em cần xác định ít nhất hai điểm thuộc đồ thị và nối chúng lại với nhau.
Ví dụ: Vẽ đồ thị của hàm số y = -x + 1.
Lời giải:
Bài tập này thường yêu cầu học sinh giải các bài toán ứng dụng liên quan đến hàm số bậc nhất. Để giải bài toán này, các em cần hiểu rõ mối liên hệ giữa các đại lượng trong bài toán và xây dựng phương trình hàm số tương ứng.
Ví dụ: Một người đi xe đạp với vận tốc 15km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Lời giải: Gọi x là thời gian đi (giờ), y là quãng đường đi được (km). Ta có hàm số y = 15x. Khi x = 2, y = 15 * 2 = 30. Vậy sau 2 giờ người đó đi được 30km.
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 4 trang 79, 80, 81 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a: Hệ số góc | Xác định độ dốc của đường thẳng |
| b: Tung độ gốc | Giao điểm của đường thẳng với trục Oy |