Chào mừng các em học sinh đến với bài giải bài tập 9.22 trang 86 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Tính bán kính đáy của hình nón có chiều cao 12 cm, đường sinh dài 13 cm. A. 5 cm B. 6 cm C. 10 cm D. 6,5 cm
Đề bài
Tính bán kính đáy của hình nón có chiều cao 12 cm, đường sinh dài 13 cm.
A. 5 cm
B. 6 cm
C. 10 cm
D. 6,5 cm
Phương pháp giải - Xem chi tiết
Dựa vào: Khi quay tam giác AOC vuông tại O một vòng quanh cạnh góc vuông OA cố định, ta được một hình nón. Khi đó:
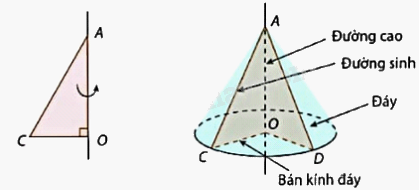
Lời giải chi tiết
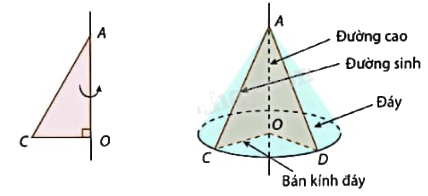
Xét tam giác AOD vuông tại O có AD = 13; AO = 12
R = OD = \(\sqrt {A{D^2} - A{O^2}} = \sqrt {{{13}^2} - {{12}^2}} = 5\) cm.
Chọn đáp án A.
Bài tập 9.22 trang 86 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tìm phương trình tiếp tuyến của một đường cong tại một điểm cho trước, hoặc xác định điều kiện để một đường thẳng là tiếp tuyến của một đường cong.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài tập 9.22 trang 86 SGK Toán 9 tập 2 một cách hiệu quả, chúng ta cần:
(Ở đây sẽ là lời giải chi tiết cho bài tập 9.22, tùy thuộc vào nội dung cụ thể của bài toán. Ví dụ:)
Ví dụ: Cho hàm số y = x2 - 2x + 3. Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm M(1; 2).
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về phương pháp tiếp tuyến, các em có thể tham khảo một số bài tập tương tự sau:
Khi giải bài tập về phương pháp tiếp tuyến, các em cần lưu ý một số điểm sau:
Phương pháp tiếp tuyến có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với bài giải chi tiết và những lưu ý trên, các em sẽ hiểu rõ hơn về phương pháp tiếp tuyến và có thể tự tin giải quyết các bài tập liên quan. Chúc các em học tập tốt!