Chào mừng bạn đến với bài học về Lý thuyết Giải bài toán bằng cách lập phương trình bậc hai Toán 9 trên giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng và thường xuyên xuất hiện trong các kỳ thi. Bài học này sẽ cung cấp cho bạn kiến thức nền tảng vững chắc và phương pháp giải quyết các bài toán một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu các bước giải bài toán bằng cách lập phương trình bậc hai, các dạng bài tập thường gặp và cách áp dụng kiến thức vào thực tế.
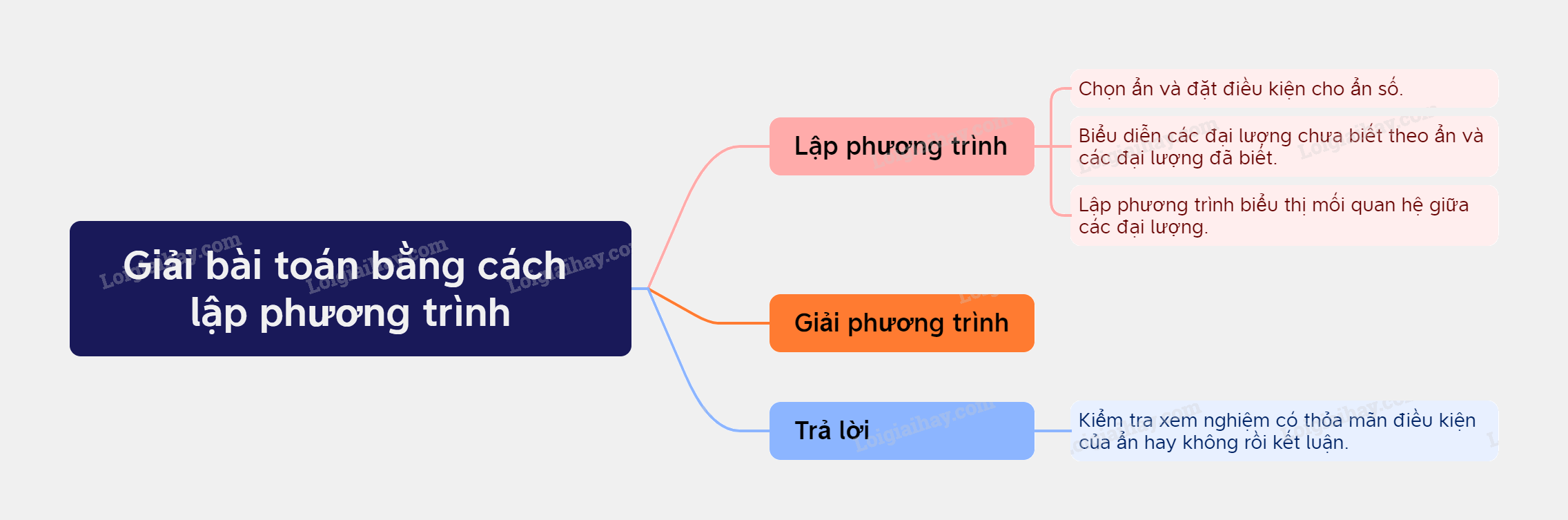
Bước 1: Lập phương trình: - Chọn ẩn và đặt điều kiện cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. - Lập phương trình biểu thị mối quan hệ giữa các đại lượng. Bước 2. Giải phương trình. Bước 3. Kiểm tra xem nghiệm có thỏa mãn điều kiện của ẩn hay không rồi kết luận.
Bước 1: Lập phương trình: - Chọn ẩn và đặt điều kiện cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. - Lập phương trình biểu thị mối quan hệ giữa các đại lượng. Bước 2. Giải phương trình. Bước 3. Kiểm tra xem nghiệm có thỏa mãn điều kiện của ẩn hay không rồi kết luận. |
Ví dụ: Một ca nô xuất phát từ một bến và có chuyển động thẳng theo hướng Đông. Cùng lúc đó, một tàu thủy rời bến và chuyển động thẳng theo hướng Nam với tốc độ lớn hơn tốc độ của ca nô 8km/h. Tính tốc độ của ca nô, biết sau một giờ kể từ lúc xuất phát, khoảng cách giữa ca nô với tàu thủy là 40km.
Lời giải:
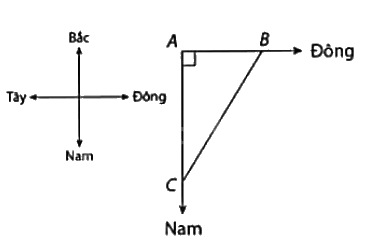
Gọi tốc độ của ca nô là \(x\left( {km/h} \right)\left( {x > 0} \right)\).
Tốc độ của tàu thủy là \(x + 8\left( {km/h} \right)\).
Gọi A là vị trí của bến, gọi B, C lần lượt là vị trí của ca nô và tàu thủy sau khi rời bến 1 giờ (như hình vẽ).
Quãng đường ca nô đi được sau 1 giờ là:
\(AB = x.1 = x\left( {km} \right)\)
Quãng đường tàu thủy đi được sau 1 giờ là:
\(AC = \left( {x + 8} \right).1 = x + 8\left( {km} \right)\)
Ca nô và tày thủy chuyển động theo hai hướng vuông góc với nhau nên tam giác ABC vuông tại A.
Ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lí Pythagore).
\(\begin{array}{l}{x^2} + {\left( {x + 8} \right)^2} - {40^2}\\{x^2} + {x^2} + 16x + 64 = 1600\\2{x^2} + 16x - 1536 = 0\\{x^2} + 8x - 768 = 0\end{array}\)
Ta có: \(\Delta ' = {4^2} + 768 = 784,\sqrt {\Delta '} = 28\).
Suy ra phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - 4 - 28}}{1} = - 32\) (loại); \({x_2} = \frac{{ - 4 + 28}}{1} = 24\) (thỏa mãn điều kiện).
Vậy tốc độ của ca nô là \(24km/h\).
Phương trình bậc hai là một trong những chủ đề quan trọng của chương trình Toán 9. Việc nắm vững lý thuyết và kỹ năng giải bài toán bằng cách lập phương trình bậc hai không chỉ giúp học sinh đạt kết quả tốt trong các kỳ thi mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề.
1. Định nghĩa: Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0, trong đó a, b, c là các số với a ≠ 0.
2. Các yếu tố của phương trình bậc hai:
3. Nghiệm của phương trình bậc hai: Nghiệm của phương trình bậc hai là giá trị của x sao cho phương trình được thỏa mãn.
1. Các bước giải bài toán bằng cách lập phương trình bậc hai:
1. Bài toán về chuyển động: Các bài toán liên quan đến vận tốc, thời gian, quãng đường.
2. Bài toán về năng suất lao động: Các bài toán liên quan đến số lượng sản phẩm, thời gian làm việc.
3. Bài toán về diện tích và chu vi: Các bài toán liên quan đến hình học, tính diện tích và chu vi của các hình.
4. Bài toán về hỗn hợp: Các bài toán liên quan đến pha trộn các dung dịch, hợp chất.
Ví dụ 1: Một người đi xe máy từ A đến B với vận tốc 40km/h. Trên đường về, người đó đi với vận tốc 30km/h. Biết thời gian cả đi lẫn về là 5 giờ. Tính quãng đường AB.
Giải:
Gọi quãng đường AB là x (km).
Thời gian đi từ A đến B là x/40 (giờ).
Thời gian đi từ B về A là x/30 (giờ).
Ta có phương trình: x/40 + x/30 = 5
Giải phương trình, ta được x = 120.
Vậy quãng đường AB là 120km.
Để củng cố kiến thức, bạn hãy tự giải các bài tập sau:
Lý thuyết Giải bài toán bằng cách lập phương trình bậc hai Toán 9 là một phần kiến thức quan trọng. Việc nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp bạn tự tin giải quyết các bài toán một cách hiệu quả. Chúc bạn học tốt!