Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1. Chúng tôi giúp bạn giải quyết mọi khó khăn trong quá trình học tập, từ đó nâng cao kết quả học tập môn Toán.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những lời giải chính xác, logic và dễ tiếp thu. Hãy cùng khám phá và chinh phục những bài toán Toán 9 một cách hiệu quả!
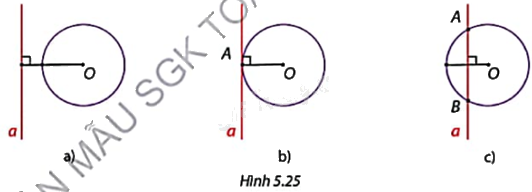
Hình 5.25 thể hiện vị trí tương đối khác nhau của đường thẳng a và đường tròn (O) khi đường thẳng a di chuyển từ ngoài về gần tâm O của đường tròn. Nêu số điểm chung của đường thẳng a và đường tròn (O) trong mỗi trường hợp.
Trả lời câu hỏi Luyện tập 2 trang 109 SGK Toán 9 Cùng khám phá
Xác định vị trí tương đối của đường thẳng a đến đường tròn (O; 7cm) nếu khoảng cách từ O đến a bằng:
a) 4cm;
b) 9cm;
c) 7cm.
Phương pháp giải:
Cho đường tròn (O; R) và đường thẳng a. Đặt d là khoảng cách từ O đến đường thẳng a. Vị trí tương đối của đường thẳng a và đường tròn (O; R) có thể được xác định dựa vào mối quan hệ giữa R và d như sau:
+ Nếu \(d > R\) thì đường thẳng a và đường tròn (O) không giao nhau.
+ Nếu \(d = R\) thì đường thẳng a và đường tròn (O) tiếp xúc nhau.
+ Nếu \(d < R\) thì đường thẳng a và đường tròn (O) cắt nhau.
Lời giải chi tiết:
a) Vì \(4 < 7\) nên đường thẳng a và đường tròn (O) cắt nhau.
b) Vì \(9 > 7\) nên đường thẳng a và đường tròn (O) không giao nhau.
c) Vì \(7 = 7\) nên đường thẳng a và đường tròn (O) tiếp xúc nhau.
Trả lời câu hỏi Hoạt động trang 107 SGK Toán 9 Cùng khám phá
Hình 5.25 thể hiện vị trí tương đối khác nhau của đường thẳng a và đường tròn (O) khi đường thẳng a di chuyển từ ngoài về gần tâm O của đường tròn. Nêu số điểm chung của đường thẳng a và đường tròn (O) trong mỗi trường hợp.
Phương pháp giải:
Quan sát hình và đếm số điểm chung của đường thẳng a đường tròn (O).
Lời giải chi tiết:
Hình 5.25a: Đường thẳng a và đường tròn (O) không có điểm chung.
Hình 5.25b: Đường thẳng a và đường tròn (O) có 1 điểm chung.
Hình 5.25c: Đường thẳng a và đường tròn (O) có 2 điểm chung.
Trả lời câu hỏi Luyện tập 1 trang 108SGK Toán 9 Cùng khám phá
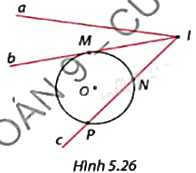
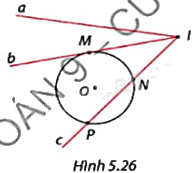
Xác định vị trí tương đối của đường tròn (O) với các đường thẳng a, b và c trong Hình 5.26. Chỉ ra tiếp điểm, giao điểm của chúng (nếu có).
Phương pháp giải:
Đường thẳng và đường tròn được gọi là cắt nhau nếu chúng có đúng 2 điểm chung phân biệt.
Đường thẳng và đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng 1 điểm chung.
Đường thẳng và đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào.
Lời giải chi tiết:
Đường thẳng a và đường tròn (O) không giao nhau.
Đường thẳng b và đường tròn (O) tiếp xúc nhau tại tiếp điểm M.
Đường thẳng c và đường tròn (O) cắt nhau tại hai điểm N và P.
Trả lời câu hỏi Vận dụng trang 105 SGK Toán 9 Cùng khám phá
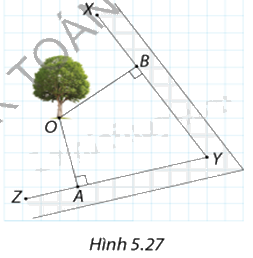
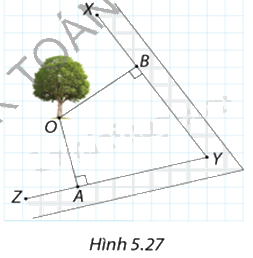
Trong Hình 5.27, mỗi ô vuông tương ứng với độ dài 1m. Có thể quây một hàng rào tròn bán kính 5m với tâm tại vị trí cây xanh O mà không cắt vào đường bao XY và YZ không?
Phương pháp giải:
+ Dựa vào định lí Pythagore tính độ dài OA, OB.
+ So sánh OA, OB với 5m để rút ra kết luận.
Lời giải chi tiết:
Ta có: \(OA = \sqrt {{4^2} + {1^2}} = \sqrt {17} \left( m \right)\), \(OB = \sqrt {{4^2} + {3^2}} = 5\left( m \right)\).
Vì \(\sqrt {17} m < 5m;5m = 5m\) nên \(OA < 5m,OB = 5m\).
Do đó, không thể quây một hàng rào tròn bán kính 5m với tâm tại vị trí cây xanh O mà không cắt vào đường bao XY và YZ.
Trả lời câu hỏi Hoạt động trang 107 SGK Toán 9 Cùng khám phá
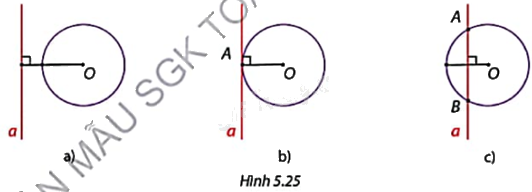
Hình 5.25 thể hiện vị trí tương đối khác nhau của đường thẳng a và đường tròn (O) khi đường thẳng a di chuyển từ ngoài về gần tâm O của đường tròn. Nêu số điểm chung của đường thẳng a và đường tròn (O) trong mỗi trường hợp.
Phương pháp giải:
Quan sát hình và đếm số điểm chung của đường thẳng a đường tròn (O).
Lời giải chi tiết:
Hình 5.25a: Đường thẳng a và đường tròn (O) không có điểm chung.
Hình 5.25b: Đường thẳng a và đường tròn (O) có 1 điểm chung.
Hình 5.25c: Đường thẳng a và đường tròn (O) có 2 điểm chung.
Trả lời câu hỏi Luyện tập 1 trang 108SGK Toán 9 Cùng khám phá
Xác định vị trí tương đối của đường tròn (O) với các đường thẳng a, b và c trong Hình 5.26. Chỉ ra tiếp điểm, giao điểm của chúng (nếu có).
Phương pháp giải:
Đường thẳng và đường tròn được gọi là cắt nhau nếu chúng có đúng 2 điểm chung phân biệt.
Đường thẳng và đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng 1 điểm chung.
Đường thẳng và đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào.
Lời giải chi tiết:
Đường thẳng a và đường tròn (O) không giao nhau.
Đường thẳng b và đường tròn (O) tiếp xúc nhau tại tiếp điểm M.
Đường thẳng c và đường tròn (O) cắt nhau tại hai điểm N và P.
Trả lời câu hỏi Luyện tập 2 trang 109 SGK Toán 9 Cùng khám phá
Xác định vị trí tương đối của đường thẳng a đến đường tròn (O; 7cm) nếu khoảng cách từ O đến a bằng:
a) 4cm;
b) 9cm;
c) 7cm.
Phương pháp giải:
Cho đường tròn (O; R) và đường thẳng a. Đặt d là khoảng cách từ O đến đường thẳng a. Vị trí tương đối của đường thẳng a và đường tròn (O; R) có thể được xác định dựa vào mối quan hệ giữa R và d như sau:
+ Nếu \(d > R\) thì đường thẳng a và đường tròn (O) không giao nhau.
+ Nếu \(d = R\) thì đường thẳng a và đường tròn (O) tiếp xúc nhau.
+ Nếu \(d < R\) thì đường thẳng a và đường tròn (O) cắt nhau.
Lời giải chi tiết:
a) Vì \(4 < 7\) nên đường thẳng a và đường tròn (O) cắt nhau.
b) Vì \(9 > 7\) nên đường thẳng a và đường tròn (O) không giao nhau.
c) Vì \(7 = 7\) nên đường thẳng a và đường tròn (O) tiếp xúc nhau.
Trả lời câu hỏi Vận dụng trang 105 SGK Toán 9 Cùng khám phá
Trong Hình 5.27, mỗi ô vuông tương ứng với độ dài 1m. Có thể quây một hàng rào tròn bán kính 5m với tâm tại vị trí cây xanh O mà không cắt vào đường bao XY và YZ không?
Phương pháp giải:
+ Dựa vào định lí Pythagore tính độ dài OA, OB.
+ So sánh OA, OB với 5m để rút ra kết luận.
Lời giải chi tiết:
Ta có: \(OA = \sqrt {{4^2} + {1^2}} = \sqrt {17} \left( m \right)\), \(OB = \sqrt {{4^2} + {3^2}} = 5\left( m \right)\).
Vì \(\sqrt {17} m < 5m;5m = 5m\) nên \(OA < 5m,OB = 5m\).
Do đó, không thể quây một hàng rào tròn bán kính 5m với tâm tại vị trí cây xanh O mà không cắt vào đường bao XY và YZ.
Chương trình Toán 9 tập 1 tập trung vào việc củng cố và mở rộng kiến thức về hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, và các ứng dụng của chúng trong giải quyết các bài toán thực tế. Trang 107, 108, và 109 của sách giáo khoa Toán 9 tập 1 chứa đựng những bài tập quan trọng, giúp học sinh rèn luyện kỹ năng giải toán và hiểu sâu hơn về các khái niệm đã học.
Các bài tập trên trang 107 thường xoay quanh việc xác định hệ số góc và tung độ gốc của đường thẳng, viết phương trình đường thẳng khi biết các yếu tố khác nhau (ví dụ: biết hai điểm mà đường thẳng đi qua, biết hệ số góc và một điểm, biết phương trình đường thẳng song song hoặc vuông góc với một đường thẳng khác). Việc nắm vững các công thức và phương pháp giải là chìa khóa để hoàn thành tốt các bài tập này.
Trang 108 tiếp tục tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến đường thẳng. Các bài tập thường yêu cầu học sinh tìm giao điểm của hai đường thẳng, xác định điều kiện để ba điểm thẳng hàng, hoặc giải các bài toán thực tế có liên quan đến hàm số bậc nhất.
Các bài tập trên trang 109 thường mang tính tổng hợp cao, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán phức tạp hơn. Các bài tập này có thể kết hợp nhiều kiến thức khác nhau, đòi hỏi học sinh phải có tư duy logic và khả năng phân tích tốt.
Bài tập: Tìm giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4.
Giải:
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình:
Thay y = 2x + 1 vào phương trình thứ hai, ta được:
2x + 1 = -x + 4
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 1, ta được:
y = 2(1) + 1 = 3
Vậy giao điểm của hai đường thẳng là (1; 3).
Để nắm vững kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các diễn đàn học tập trực tuyến để trao đổi kinh nghiệm và học hỏi từ những người khác.
Giải câu hỏi trang 107, 108, 109 SGK Toán 9 tập 1 là một bước quan trọng trong quá trình học tập môn Toán của bạn. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ tự tin hơn trong việc giải quyết các bài tập và đạt được kết quả tốt nhất.