Chào mừng các em học sinh đến với bài giải bài tập 5.18 trang 114 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Từ điểm M nằm ngoài đường tròn (O; 5cm), \(MO = 13cm\), vẽ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). a) Tính độ dài MA và MB. b) Cho C là điểm bất kì thuộc đường tròn (O) và nằm trong góc AOB. Tiếp tuyến tại C của đường tròn cắt MA tại N và cắt MB tại P. Tính chu vi \(\Delta MNP\).
Đề bài
Từ điểm M nằm ngoài đường tròn (O; 5cm), \(MO = 13cm\), vẽ hai tiếp tuyến MA, MB (A, B là các tiếp điểm).
a) Tính độ dài MA và MB.
b) Cho C là điểm bất kì thuộc đường tròn (O) và nằm trong góc AOB. Tiếp tuyến tại C của đường tròn cắt MA tại N và cắt MB tại P. Tính chu vi \(\Delta MNP\).
Phương pháp giải - Xem chi tiết
a) + Chứng minh tam giác MAO vuông tại A. Áp dụng định lí Pythagore vào tam giác MAO tính MA.
+ MA và MB là tiếp tuyến của đường tròn (O) nên \(MA = MB\).
b) + Sử dụng tính chất của hai tiếp tuyến cắt nhau chứng minh \(NC = NA\), \(CP = BP\).
+ Chu vi tam giác MNP:
\(MN + NP + MP\)\( = MN + NC + CP + MP\)\( = MN + NA + MP + PB\)\( = MA + MB\)
Lời giải chi tiết
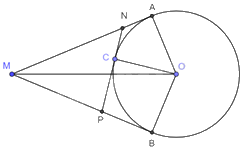
a) Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên tam giác MAO vuông tại A.
Do đó, \(M{A^2} + A{O^2} = M{O^2}\) (định lí Pythagore) nên
\(MA = \sqrt {M{O^2} - A{O^2}} = \sqrt {{{13}^2} - {5^2}} = 12\left( {cm} \right)\).
Vì MA và MB là tiếp tuyến của đường tròn (O) nên
\(MA = MB = 12cm\).
b) Vì NA và NC là tiếp tuyến của đường tròn (O) nên \(NC = NA\).
Vì CP và PB là tiếp tuyến của đường tròn (O) nên \(CP = BP\).
Chu vi tam giác MNP là:
\(MN + NP + MP\)\( = MN + NC + CP + MP\)\( = MN + NA + MP + PB\)\( = MA + MB\)\( = 12 + 12\)\( = 24\left( {cm} \right)\)
Bài tập 5.18 trang 114 SGK Toán 9 tập 1 yêu cầu chúng ta tìm hiểu về phương pháp tiếp tuyến của một đường thẳng với một đường tròn. Đây là một kiến thức quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa đường thẳng và đường tròn.
Để giải bài tập 5.18, chúng ta cần xác định được các yếu tố sau:
(Giả sử bài tập 5.18 có nội dung cụ thể về một đường tròn và một đường thẳng. Phần này sẽ trình bày lời giải chi tiết dựa trên nội dung đó. Ví dụ:)
Cho đường tròn (O; 5cm) và đường thẳng d. Biết khoảng cách từ O đến d là 3cm. Chứng minh rằng d không phải là tiếp tuyến của đường tròn (O).
Lời giải:
Vì khoảng cách từ O đến d là 3cm, mà bán kính của đường tròn (O) là 5cm. Do đó, 3cm < 5cm. Điều này có nghĩa là đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt. Vậy d không phải là tiếp tuyến của đường tròn (O).
Ngoài bài tập 5.18, còn rất nhiều bài tập tương tự liên quan đến phương pháp tiếp tuyến. Dưới đây là một số dạng bài tập thường gặp:
Để giải các bài tập này, chúng ta cần nắm vững lý thuyết về tiếp tuyến, tính chất của tiếp tuyến và điều kiện để một đường thẳng là tiếp tuyến của đường tròn. Ngoài ra, chúng ta cũng cần rèn luyện kỹ năng vẽ hình và phân tích bài toán một cách chính xác.
Phương pháp tiếp tuyến không chỉ có ý nghĩa trong toán học mà còn có nhiều ứng dụng trong thực tế. Ví dụ:
Để củng cố kiến thức về phương pháp tiếp tuyến, các em có thể tự giải các bài tập sau:
Bài tập 5.18 trang 114 SGK Toán 9 tập 1 là một bài tập quan trọng giúp chúng ta hiểu rõ hơn về phương pháp tiếp tuyến. Hy vọng rằng với lời giải chi tiết và các kiến thức bổ sung trên đây, các em sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.