Chào mừng các em học sinh đến với bài giải bài tập 7.12 trang 38 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng cung cấp các bài tập tương tự để các em luyện tập và củng cố kiến thức.
Cho tam giác nhọn ABC có AD, BE, CF là đường cao và H là trực tâm. Chứng minh rằng a) Tứ giác AEHF, BDHF và CDHE là các tứ giác nội tiếp b) DA là đường phân giác của góc FDE.
Đề bài
Cho tam giác nhọn ABC có AD, BE, CF là đường cao và H là trực tâm. Chứng minh rằng
a) Tứ giác AEHF, BDHF và CDHE là các tứ giác nội tiếp
b) DA là đường phân giác của góc FDE.
Phương pháp giải - Xem chi tiết
Đọc kĩ dữ kiện để vẽ hình
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Áp dụng hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
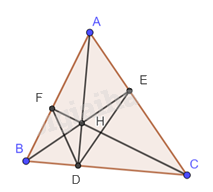
a) Ta có \(\widehat {AEH} = \widehat {AFH} = {90^o}\) (Do CF và BE là đường cao)
suy ra AEHF là tứ giác nội tiếp.
Chứng minh tương tự BDHF và CDHE là các tứ giác nội tiếp
b) Theo phần a ta có BDHF nội tiếp nên \(\widehat {ABE} = \widehat {FDA}\)
DHEC nội tiếp nên \(\widehat {ADE} = \widehat {FCA}\).
Lại có \(\widehat {ABE} = \widehat {FCA}\) (cùng phụ \(\widehat {BAC}\))
Suy ra \(\widehat {FDA} = \widehat {ADE}\) hay AD là đường phân giác của góc FDE.
Bài tập 7.12 trang 38 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc xác định hàm số, tìm điểm thuộc đồ thị hàm số, hoặc giải các bài toán ứng dụng liên quan đến hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh tránh được những sai sót không đáng có và tìm ra phương pháp giải phù hợp.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các hệ số. Để giải bài tập liên quan đến hàm số bậc nhất, học sinh cần nắm vững các kiến thức sau:
Để minh họa, chúng ta sẽ cùng nhau giải một ví dụ cụ thể về bài tập 7.12 trang 38 SGK Toán 9 tập 2. (Ở đây cần có nội dung bài tập cụ thể và lời giải chi tiết, ví dụ:)
Ví dụ: Cho hàm số y = 2x - 1. Tìm tọa độ giao điểm của đồ thị hàm số với đường thẳng y = x + 2.
Lời giải:
Ngoài bài tập 7.12, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, học sinh cần luyện tập thường xuyên. Các em có thể tìm các bài tập tương tự trong SGK, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Ngoài hàm số bậc nhất, học sinh cũng nên tìm hiểu về các loại hàm số khác như hàm số bậc hai, hàm số mũ, hàm số logarit. Việc nắm vững kiến thức về các loại hàm số khác nhau sẽ giúp các em giải quyết các bài toán phức tạp hơn.
Hy vọng với bài giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài tập 7.12 trang 38 SGK Toán 9 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!