Chào mừng các em học sinh đến với bài giải bài tập 4.16 trang 88 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
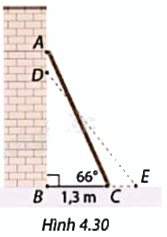
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho. Một chiếc thang AC được dựng vào một bức tường thẳng đứng (Hình 4.30). a) Ban đầu, khoảng cách từ chân thang đến tường là \(BC = 1,3m\) và góc tạo bởi thang và phương nằm ngang là \(\widehat {ACB} = {66^o}\), tính độ dài của thang. b) Nếu đầu A của thang bị trượt xuống 40cm đến vị trí D thì góc DEB tạo bởi thang và phương nằm ngang khi đó bằng bao nhiêu?
Đề bài
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
Một chiếc thang AC được dựng vào một bức tường thẳng đứng (Hình 4.30).
a) Ban đầu, khoảng cách từ chân thang đến tường là \(BC = 1,3m\) và góc tạo bởi thang và phương nằm ngang là \(\widehat {ACB} = {66^o}\), tính độ dài của thang.
b) Nếu đầu A của thang bị trượt xuống 40cm đến vị trí D thì góc DEB tạo bởi thang và phương nằm ngang khi đó bằng bao nhiêu?
Phương pháp giải - Xem chi tiết
a) Tam giác ABC vuông tại B nên \(BC = AC.\cos ACB\), từ đó tính được AC.
b)
+ Tam giác ABC vuông tại B nên \(AB = BC.\tan ACB\). Do đó, \(BD = AB - AD\).
+ Ta có: \(AC = DE\).
+ Tam giác BDE vuông tại B nên \(\sin E = \frac{{BD}}{{DE}}\), do đó tính được góc E.
Lời giải chi tiết
a) Tam giác ABC vuông tại B nên
\(BC = AC.\cos ACB\), suy ra:
\(AC = \frac{{BC}}{{\cos ACB}} = \frac{{1,3}}{{\cos {{66}^o}}} \approx 3,2\left( m \right)\).
Vậy độ dài chiếc thang khoảng 3,2m.
b) Tam giác ABC vuông tại B nên
\(AB = BC.\tan ACB = 1,3.\tan {66^o} \approx 2,9\left( m \right)\).
Do đó, \(BD = AB - AD \approx 2,9 - 0,4 \approx 2,5\left( m \right)\).
Ta có: \(AC = DE \approx 3,2m\).
Tam giác BDE vuông tại B nên
\(\sin E = \frac{{BD}}{{DE}} \approx \frac{{2,5}}{{3,2}}\), do đó \(\widehat E \approx {51^o}23'\).
Bài tập 4.16 trang 88 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, và các tính chất của hàm số.
Hàm số bậc nhất có dạng y = ax + b (với a ≠ 0).
Để giải các bài toán liên quan đến hàm số bậc nhất, chúng ta thường sử dụng các phương pháp sau:
Trước khi đi vào giải chi tiết, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài toán 4.16 thường yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết của bài tập 4.16, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ, nếu bài toán yêu cầu tìm hàm số bậc nhất đi qua hai điểm A(x1, y1) và B(x2, y2), lời giải sẽ trình bày các bước tính hệ số góc a và tung độ gốc b.)
Để giúp các em hiểu rõ hơn về cách giải bài tập 4.16, chúng ta sẽ xem xét một số ví dụ minh họa:
Ví dụ 1: Tìm hàm số bậc nhất y = ax + b biết đồ thị của hàm số đi qua điểm A(1; 2) và có hệ số góc a = 3.
Lời giải: Vì hàm số đi qua điểm A(1; 2) nên ta có: 2 = 3 * 1 + b => b = -1. Vậy hàm số cần tìm là y = 3x - 1.
Bài tập tương tự:
Ngoài việc giải bài tập 4.16, các em có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, chẳng hạn như tính toán chi phí, dự báo doanh thu, hoặc mô tả sự thay đổi của các đại lượng vật lý.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em nên luyện tập thêm các bài tập khác trong SGK Toán 9 tập 1 và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em rèn luyện và nâng cao khả năng giải toán.
Hy vọng với bài giải chi tiết và các ví dụ minh họa trên, các em đã hiểu rõ cách giải bài tập 4.16 trang 88 SGK Toán 9 tập 1. Chúc các em học tập tốt!