Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 1 trang 83, 84 SGK Toán 9 tập 1. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho \(\Delta ABC\) vuông tại A như Hình 4.17. Xác định tên các góc nhọn ở các ô ?: Vì \(\frac{b}{a} = \cos ?\) nên \(b = a.\cos ?\); Vì \(\frac{b}{a} = \sin ?\) nên \(b = a.\sin ?\); Vì \(\frac{b}{c} = \tan ?\) nên \(b = c.\tan ?\); Vì \(\frac{b}{c} = \cot ?\) nên \(b = c.\cot ?\);
Trả lời câu hỏi Hoạt động 1 trang 83 SGK Toán 9 Cùng khám phá
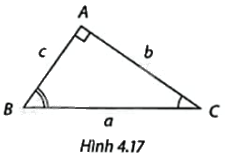
Cho \(\Delta ABC\) vuông tại A như Hình 4.17. Xác định tên các góc nhọn ở các ô ?:
Vì \(\frac{b}{a} = \cos ?\) nên \(b = a.\cos ?\);
Vì \(\frac{b}{a} = \sin ?\) nên \(b = a.\sin ?\);
Vì \(\frac{b}{c} = \tan ?\) nên \(b = c.\tan ?\);
Vì \(\frac{b}{c} = \cot ?\) nên \(b = c.\cot ?\);
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Vì \(\frac{b}{a} = \cos C\) nên \(b = a.\cos C\);
Vì \(\frac{b}{a} = \sin B\) nên \(b = a.\sin B\);
Vì \(\frac{b}{c} = \tan B\) nên \(b = c.\tan B\);
Vì \(\frac{b}{c} = \cot C\) nên \(b = c.\cot C\);
Trả lời câu hỏi Luyện tập 1 trang 84SGK Toán 9 Cùng khám phá
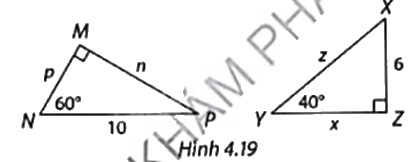
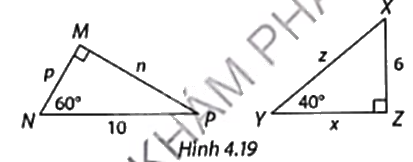
Tính các độ dài n, p, x, z trong Hình 4.19. Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
\(\Delta \)MNP vuông tại M nên
\(p = NP\cos N = 10\cos {60^o} = 10.\frac{1}{2} = 5\),
\(n = NP\sin N = 10\sin {60^o} = 10.\frac{{\sqrt 3 }}{2} \approx 8,66\)
Tam giác XYZ vuông tại Z nên
\(x = 6\cot {40^o} \approx 7,15\), \(z = \frac{6}{{\sin {{40}^o}}} \approx 9,33\).
Trả lời câu hỏi Vận dụng 1 trang 84 SGK Toán 9 Cùng khám phá
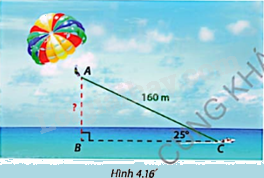
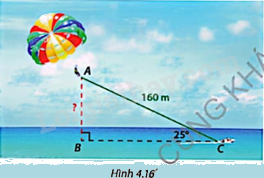
Quay lại bài toán ở phần Khởi động. Góc tạo bởi dây kéo dù bay và phương ngang là \(\widehat {ACB} = {25^o}\).
a) Tính độ cao AB của dù bay nếu dây kéo AC dài 160m.
b) Nếu muốn bay cao 75m thì dây kéo phải dài bao nhiêu mét?
Làm tròn kết quả đến hàng phần mười mét.
Bài toán khởi động: Ca nô dù bay là một trò chơi thể thao biển được ưa chuộng, trong đó người chơi được đeo dù và được ca nô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao như Hình 4.17.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
a) Tam giác ABC vuông tại B nên
\(AB = AC.\sin C = 160.\sin {25^o} \approx 67,6\left( m \right)\)
b) Ta có: \(AB = 75m\).
Tam giác ABC vuông tại B nên \(AB = AC.\sin C\) suy ra \(AC = \frac{{AB}}{{\sin C}} = \frac{{75}}{{\sin {{25}^o}}} \approx 177,5\left( m \right)\).
Trả lời câu hỏi Hoạt động 1 trang 83 SGK Toán 9 Cùng khám phá
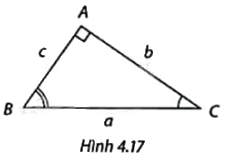
Cho \(\Delta ABC\) vuông tại A như Hình 4.17. Xác định tên các góc nhọn ở các ô ?:
Vì \(\frac{b}{a} = \cos ?\) nên \(b = a.\cos ?\);
Vì \(\frac{b}{a} = \sin ?\) nên \(b = a.\sin ?\);
Vì \(\frac{b}{c} = \tan ?\) nên \(b = c.\tan ?\);
Vì \(\frac{b}{c} = \cot ?\) nên \(b = c.\cot ?\);
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Vì \(\frac{b}{a} = \cos C\) nên \(b = a.\cos C\);
Vì \(\frac{b}{a} = \sin B\) nên \(b = a.\sin B\);
Vì \(\frac{b}{c} = \tan B\) nên \(b = c.\tan B\);
Vì \(\frac{b}{c} = \cot C\) nên \(b = c.\cot C\);
Trả lời câu hỏi Luyện tập 1 trang 84SGK Toán 9 Cùng khám phá
Tính các độ dài n, p, x, z trong Hình 4.19. Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
\(\Delta \)MNP vuông tại M nên
\(p = NP\cos N = 10\cos {60^o} = 10.\frac{1}{2} = 5\),
\(n = NP\sin N = 10\sin {60^o} = 10.\frac{{\sqrt 3 }}{2} \approx 8,66\)
Tam giác XYZ vuông tại Z nên
\(x = 6\cot {40^o} \approx 7,15\), \(z = \frac{6}{{\sin {{40}^o}}} \approx 9,33\).
Trả lời câu hỏi Vận dụng 1 trang 84 SGK Toán 9 Cùng khám phá
Quay lại bài toán ở phần Khởi động. Góc tạo bởi dây kéo dù bay và phương ngang là \(\widehat {ACB} = {25^o}\).
a) Tính độ cao AB của dù bay nếu dây kéo AC dài 160m.
b) Nếu muốn bay cao 75m thì dây kéo phải dài bao nhiêu mét?
Làm tròn kết quả đến hàng phần mười mét.
Bài toán khởi động: Ca nô dù bay là một trò chơi thể thao biển được ưa chuộng, trong đó người chơi được đeo dù và được ca nô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao như Hình 4.17.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
a) Tam giác ABC vuông tại B nên
\(AB = AC.\sin C = 160.\sin {25^o} \approx 67,6\left( m \right)\)
b) Ta có: \(AB = 75m\).
Tam giác ABC vuông tại B nên \(AB = AC.\sin C\) suy ra \(AC = \frac{{AB}}{{\sin C}} = \frac{{75}}{{\sin {{25}^o}}} \approx 177,5\left( m \right)\).
Mục 1 trang 83, 84 SGK Toán 9 tập 1 thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai, và các ứng dụng của chúng. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản như:
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 83, 84 SGK Toán 9 tập 1, chúng tôi sẽ trình bày chi tiết lời giải của từng bài tập:
Để xác định hệ số a, b của hàm số y = ax + b, các em có thể sử dụng các phương pháp sau:
Để vẽ đồ thị hàm số y = ax + b, các em thực hiện các bước sau:
Để tìm giao điểm của hai đường thẳng y = a₁x + b₁ và y = a₂x + b₂, các em giải hệ phương trình:
Nghiệm của hệ phương trình là tọa độ của giao điểm.
Sau khi đã nắm vững lý thuyết và phương pháp giải, các em nên luyện tập thêm các bài tập tương tự để củng cố kiến thức. Các em có thể tìm thấy thêm nhiều bài tập trong sách bài tập Toán 9 tập 1, các đề thi thử và trên các trang web học toán online.
Để học tốt môn Toán 9, các em cần:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 83, 84 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!