Chào mừng các em học sinh đến với bài giải bài tập 5.38 trang 127 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
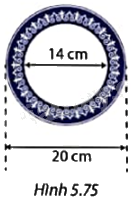
Tính chu vi đĩa sứ và diện tích phần viền tráng men xanh của đĩa sứ trong Hình 5.75.
Đề bài
Tính chu vi đĩa sứ và diện tích phần viền tráng men xanh của đĩa sứ trong Hình 5.75.
Phương pháp giải - Xem chi tiết
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; R) và (O; r) (với \(r < R\)):
\({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\).
Chu vi C của đường tròn bán kính R là: \(C = 2\pi R\).
Lời giải chi tiết
Chu vi đĩa sứ là: \(C = 20\pi \left( {cm} \right)\).
Diện tích phần viền tráng men xanh của đĩa sứ là:
\(S = \left[ {{{\left( {\frac{{20}}{2}} \right)}^2} - {{\left( {\frac{{14}}{2}} \right)}^2}} \right]\pi = 51\pi \left( {c{m^2}} \right)\).
Bài tập 5.38 trang 127 SGK Toán 9 tập 1 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng và ứng dụng của nó trong việc tìm điểm giao nhau của các đường thẳng.
Đề bài thường đưa ra một tình huống cụ thể, ví dụ như một vật thể di chuyển trên một đường thẳng, hoặc một hệ thống các đường thẳng giao nhau. Yêu cầu của bài toán là tìm phương trình đường thẳng thỏa mãn các điều kiện cho trước, hoặc xác định tọa độ giao điểm của các đường thẳng.
Đề bài: Cho hai điểm A(1; 2) và B(3; 4). Hãy tìm phương trình đường thẳng đi qua hai điểm này.
Giải:
Ngoài bài tập 5.38, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất. Một số dạng bài tập phổ biến bao gồm:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 5.38 trang 127 SGK Toán 9 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và áp dụng vào các bài tập tương tự.